Class 11 Maths NCERT solutions of Chapter 12 three dimensional coordinate geometry exercise 12.1
In class VI, VII and VIII you had learned how to show the integers in the number line, which was the beginning of the co-ordinate geometry in one dimension. In class IX and X, you would have got the idea of two-dimensional coordinate geometry. Two-dimensional geometry means showing the magnitudes of two physical quantities in the cartesian planes made by two number lines intersecting each other at 90⁰. The vertical line is called y-axis and the horizontal line is known as x-axis, on the same way in class XI we are assigned the elements based on three-dimensional coordinate geometry in which three axis x,y, and z exist perpendicular to each other in which three physical quantities related to one another are shown.Here you can study in free of cost NCERT solutions, CBSE important maths questions, guess papers, sample papers of maths and science, articles on science and maths, blog post for your carrier etc.
Class 11 Maths NCERT solutions of Chapter 12 three dimensional coordinate geometry exercise 12.1
Exercise 12.1
1- Find the coordinate of the points which divides the line segment joining the points (–2,3,5) and (1,–4, 6) in the ratio
(i) 2 : 3 internally (ii) 2 : 3 externally
Solution.
(i) The coordinates of the points C(x,y,z) that divides the line segment
A(–2,3,5) and B(1,–4,6) internally in the ratio m: n.
Thus the required coordinates of the point C are
(ii)The coordinates of the points C(x,y,z) that divides the line segment
A(–2,3,5) and B(1,–4,6) externally in the ratio m: n.
x = – 8, y = 17, z = 3
Hence the required coordinates of point C are (–8,17,3) that divides AB externally in the ratio of 2: 3.
Q2.Given that P(3,2,–4) , Q(5,4,–6) and R(9,8,–10) are collinear. Find the ratio in which Q divides PR.
Answer.Let the point Q(5,4,–6) divide the line segment joining points P(3,2,–4) and R (9,8,–10) in the ratio of k : 1.
The section formula when the point (x,y,z) divides the line segment joining two points is following
5k + 5 = 9k + 3
4k = 2
The line segment PR is divided by the point Q in the ratio of 1 : 2.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Q3. Find the ratio in which the YZ plane divides the line segment formed by joining the points (–2,4,7) and (3,–5,8).
Answer. Let the YZ plane divides the line segment formed by joining the points (–2,4,7) and (3,–5,8) in the ratio of k : 1
Since the x coordinates of the point of intersection is 0, so let the coordinates of the point of intersection is (0,y,z)
So YZ plane divides the given line segment in the ratio of 2 : 3
Q4. Using section formula ,show that the points A(2,–3,4), B(–1,2,1) and
are collinear.
Answer.
The given points are A(2,–3,4), B(–1,2,1) and
Let B(–1,2,1) divides the line segment AC in the ratio of k :1
From each equation we get k = –3
So, k= –3 mean B(–1,2,1) divides AC in the ratio of 3 : 1 and minus sign of k shows that B divides AC externally.
Q5.Find the coordinates of the points which trisect the line segment joining the points P(4,2,–6) and Q(10,–16,6).
Answer.Let R(a,b,c) and S(d,e,f) are the points which trisect PQ.
As shown in the diagram R(a,b,c) divides the line segment PQ in the ratio of 1 : 2, therefore applying the section formula
Substituting the value of k= 1/2 and coordinates of points P(4,2,–6) and Q(10,–16,6)
(a,b,c) = (6, –4, –2)
Hence coordinates of R are (6,–4, –2)
S is the midpoint of the points R(6,–4, –2) and Q(10,–16,6), therefore the coordinates of S will be as follows
(d,e,f) = (8, –10, 2)
Therefore R(6,–4,–2) and S(8,–10, 2) trisects the line segment PQ
Miscellaneous Exercise
Q1. Three vertices of a parallelogram ABCD are A(3, –1,2), B(1,2,–4) and C(–1,1,2).Find the coordinates of the fourth vertex.
Answer. Let the coordinates of the fourth vertex (D) are (x,y,z)
As we know the diagonals of a parallelogram bisect each other
∴ The midpoint of AC = Midpoint of BD
The coordinates of midpoint O from the coordinates of A and C
………..(i)
The coordinates of midpoint O from the coordinates of B and D
……………..(ii)
From (i) and (ii)
x = 1, y = –2, z = 8
Hence the coordinates of the fourth vertex D are (1,–2, 8)
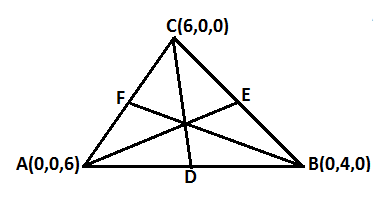
Q2. Find the lengths of the medians of the triangle with vertices A(0,0,6), B(0,4,0) and C(6,0,0).
Answer. Let the ΔABC has the medians DC, AE and BF
D, E and F will be the midpoints of AB, BC and AC respectively
∴ The coordinates of D, E and F will be as follows
Therefore the coordinates of D , E and F are (0,2,3), (3,2,0) and (3,0,3) respectively and we are given the coordinates A(0,0,6), B(0,4,0) and C(6,0,0) ,so lengths of medians DC, AE and BF are calculated as follows.
Applying the distance formula
Hence the length of the medians of the given triangle are 7unit,7 unit and √34 unit.
Q3. If the origin is the centroid of the triangle PQR with vertices P(2a,2,6),Q(–4,3b,–10) and R(8,14,2C), then find the value of a, b and c.
Answer. The coordinates of the centroid of the triangle whose vertes are given by the following formula
We are given that the origin(0,0,0) is the centroid
Thus,the value of a,b and c are respectively.
Q4. Find the coordinates of a point on the y-axis which are at a distance of 5√2 from point P(3,–2,5).
Answer. If a point is on the y-axis then its x and z coordinates will be zero, so let the coordinates of the point are (0,a,0).
We are given distance 5√2 from the point P(3,–2,5) from the point(0, a,0) on the y-axis, so applying the distance formula.
Squaring both sides
50 = a² + 4a + 38
a² + 4a – 12 = 0
a² + 6a– 2a– 12 =0
a (a + 6)– 2(a + 6) = 0
(a + 6)(a – 2) = 0
a = –6, 2
Therefore the coordinates of the point on the y-axis are (0,–6,0) or (0,2,0)
Q5. A point R with x coordinate 4 lies on the line segment joining the points P(2,–3,4) and Q(8,0,10). Find the coordinates of R.
Answer. Let R divides the line segment PQ in the ratio of k : 1
The coordinates of the point (x,y,z) dividing the line segment joining the points are given by
We are given here x coordinate only i.e 4 and the points P(2,–3,4) and Q(8,0,10)
Q6. If A and B be the two points (3,4,5) and (–1,3,7) respectively, find the equation of set of points P such that PA² + PB² = k², where k is a constant.
Answer. Let (x,y,z) are the coordinates of the point P satisfying the given condition PA² + PB² = k².
Applying the distance formula
PA² = (x–3)² + (y–4)² +(z–5)² = x² + y² + z² –6x –8y –10z + 50
PA² =x² + y² + z² –6x –8y –10z + 50………(i)
PB² = (x+1)² + (y–3)² +(z+7)²=x² + y² + z² +2x –6y+14z +59
PB² = x² + y² + z² +2x –6y+14z +59……….(ii)
PA² + PB² =k²
x² + y² + z² –6x –8y –10z + 50 + x² + y² + z² +2x –6y+14z +59 =k²
2x² + 2y² + 2z² –4x –14y +4z+109 =k²
2x² + 2y² + 2z² –4x –14y +4z = k² –109
Dividing the equation by 2
So,this is the required equation
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT Solutions for Class 11 Physics
chapter 3-Motion in a Straight Line
NCERT Solutions for Class 11 Chemistry
Chapter 1-Some basic concepts of chemistry
NCERT Solutions for Class 11 Biology
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution