NCERT Solutions class 10 exercise 12.3 of chapter 12-Areas related to circle
NCERT Solutions class 10 exercise 12.3 of chapter 12-Areas related to circle will help the students of 9 class in the preparation of CBSE board exams. All solutions are the solutions of the unsolved questions of class 9 NCERT text book. Each solution is solved by a step by step method so,the students will not face any kind of problem. The solutions are created by an expert math teacher. You can also study here NCERT solutions of maths and science, sample papers, solutions of previous year question papers, tips for competitive exams and online jobs.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Download pdf of NCERT Solutions of class 10 maths chapter 12-Areas related to circles
Pdf-NCERT solutions of class 10 maths chapter 12-Areas related to Circle
NCERT Solutions for Class 10 Maths Chapter 12-Areas related to circles
Exercise 12.1- Area Related to Circle
Exercise 12.2- Areas related to Circle
Exercise 12.3-Areas Related to the Circle
Solution of Latest Sample paper Class 10 maths for Term 1 2021 CBSE board
Q1.Find the area of the shaded region in the given figure,if PQ = 24 cm, PR = 7 cm, and O is the centre of the circle.
Ans. We are given PQ = 24 cm. PR = 7 cm
O is the centre of the circle given to us,so QR is the diameter of the circle
∴ QPR = 90° ( angle made on the semicircle)
Applying the pythogorus theorem in ΔQPR
QR² = PR² + PQ²
= 24² + 7² = 576 + 49 = 625
QR = 25 cm
So, the diameter of the circle is = 25 cm
Radius of the circle is = 25/2 = 12.5 cm
Area of triangle
= 84
Area of the triangle = 84 sq.cm
Area of semicircle PQR
Area of shaded region = Area of the semicircle QPROQ – Area of triangle QPR
Area of the shaded region
Q2. Find the area of the shaded region in the given figure . If radii of two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC =40°.
Ans. We are given the radii of two concentric circles 7 cm and 14 cm subtending a
Area of the shaded region AFCDEB = Area of sector OAFC – Area of sector OBED
Area of the sector is given as
Area of sector OAFC
Area of sector OBED
Area of the shaded region AFCDEB
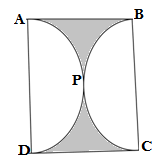
Q3. Find the area of shaded region in the given figure ,if ABCD is a square of side 14 cm and APC and BPC are semicircles
Ans. We are given side of square = 14 cm and semicircle APC and BPC
Area of shaded region = Area of the square ABCD – Area of two semicircles APC and BPC
Radii of two semicircles are = 14/2 = 7 cm
Area of the square ABCD = side × side = 14 × 14 = 196 cm²
Area of two semicircles APC and BPC = 2×πr²/2 = (22/7)× 7×7= 22×7 =154 cm²
Area of shaded region = 196 – 154 = 42 cm²
Purchase,Mobiles,Laptops,Desktop and accesories at low EMI’s
Q4. Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral OAB of side 12 cm as centre.
Ans.
We are given the radius of arc = 6 cm
Side of square = 12 cm
Area of shaded region = Area of circle formed after extending the arc D to C – Area of sector DOC + Area of equilateral ΔAOB
Area of circle = πr² = (22/7)×6×6=(792/7) cm²
Area of sector DOC
Area of equilateral ΔAOB = [(Side)²/4] √3
= [(12)²/4]√3=(144/4)√3= 36√3 cm²
Area of shaded region
Please follow us on pintrest
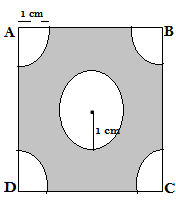
Q5. From each corner of the square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the given figure. Find the remaining portion of the square.[use π = 22/7]
Ans. We are given radii of 4 quadrant of circle created on the verteces of the square,and radii of the circle at the centre of the circle 1 cm and side of square 4 cm
Area of the shaded region = Area of the square – Area of 4 quadrant – Area of circle
= Side × Side – 4×(πr²)/4- πr²
= 4 × 4 – (22/7)×1² – (22/7)1²
= 16 – 22/7 – 22/7
=16 – 44/7
=(112-44)/7
=68/7
Hence the area of shaded region is (68/7) cm²
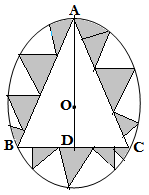
Q6.In a circular table cover of radius 32 cm ,a design is formed leaving an equilateral triangle ABC in the middle as shown in the given figure .Find the area of the design (shaded region)[use π = 22/7]
Ans.We are given radius of the circle 32 cm and three designs leaving an equilateral triangle(ABC) at the middle.
Drawing AD median that is AD ⊥ BC
The centre O of the circle is the centroid of the triangle
We know the cetroid of te triangle divides each median into 1 : 2 and bisects the sides of triagle ABC.
AO = (2/3) of AD
32 = (2/3) of AD
AD = 48 cm
BD = BC/2
Applying pythogorus theorem in ΔABD
AB² = BD² + AD²
AB = BC(sides of equilateral triangle)
BC² = (BC/2)² + AD²
48² = BC² – (BC/2)²
48² = (4BC² -BC²)/4 = 3BC²/4
BC² = (4× 48× 48)/3
BC = 2×4×4√3= 32√3 cm
Area of equilateral triangle ABC
= 16×16×3√3
=768√3 cm²
Area of circle =πr² = (22/7)×32×32 =(22528/7) cm²
Hence the area of design = [(22528/7) -768√3 ]cm²
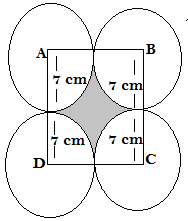
Q7.In the given figure ,ABCD is a square of side 14 cm with centres A,B,C and D, four circles are drawn such that each circles toches externally two of the remaining three circles. Find the area of shaded region.
Ans. We are given the side of square = 14 cm
Radii of each quadrant of the circle is = 14/2 = 7 cm
The area of shaded region = Area of the square – Area of quadrants inside the square
= Side ×Side – 4[1/4 (πr²)]
= 14 × 14 – (22/7) ×7×7
= 196 -154 = 42
Hence area of the shaded region is 42 cm²
Q8. The given figure depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m long .If the track is 10 m wide ,find:
(i) The distance around the track along its inner edge
(ii) The area of the track
[use π = 22/7]
Ans.
(i) The distance around the track along its inner edge = Length of rectangular part + Length of both semicircular parts
The distance around the track along its inner edge = 106×2 + (2πr/2 )×2
= 212 + 2×(22/7) ×30
= 212 + 1320/7
= (1484 + 1320)/7
=2804/7 cm
(ii) The area of the track = Area of both rectangular paths + Area of both circular path
The area of the track = 2×106 ×10 + 2×π(40²- 30²)/2
= 2120 + (22/7)( 1600 -900)
= 2120 + (22/7) 700
=2120 + 2200 =4320 m²
Q9.In the given figure ,AB and CD are two diameter of circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle .If OA = 7 cm,find the area of shaded region.
[use π = 22/7]
Ans. The area of shaded region = Area of the segments formed by the chords DC and AC + Area of the circle of diameter BO (7 cm)
Area of the segments formed by the chords DC and AC = Area of the sector OAB – Area of the right ΔOBC
=2[ (πr²/4) – (1/2) OC ×OD]
=2 [(22/7) ×7×7/4 – (1/2) ×7×7]
=2[77/2 – 49/2]
=2 [28/2 ]= 28 cm²
Area of the circle of diameter OB
= πr² = (22/7) ×(7/2)(7/2) = 77/2 = 38.5 cm²
The area of shaded region = 28 + 38.5 = 66.5 cm²
Q10.The area of an equilateral triangle ABC is 17320.5 cm², with each vertex of the triangle as centre ,a circle is drawn with a radius equal to half the length of the side of the triangle (see the given figure). Find the area of the shaded region
[use π= 3.14 and √3 = 1.73205]
Ans.
Let the side of the equilateral triangle be a.
Area of equilateral triangle = 17320.5 cm2
a²√3/4 = 17320.5
a² = 17320.5×4/√3
a² = 17320.5×4/1.73205
a = 200
Length of side of the triangle is 200 cm
Radii of each circle is 200/2=100 cm
What are the physical and chemical properties of metals?
NCERT Solutions of all chapters of Maths for Class 10 from Chapters 1 to 15
NCERT Solutions Class 10 Science from chapter 1 to 16
You can also study
Science and Maths NCERT solutions for Class 9 ,10 and 11 classes
You can compensate us by donating any amount of money for our survival
Our Paytm NO 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution