NCERT Solutions Class 9 Maths Exercise 8.2 of chapter 8- Quadrilateral
NCERT Solutions Class 9 Maths Exercise 8.2 of chapter 8-Quadrilateral are the solutions of unsolved questions of exercise 8.2 of the NCERT maths text book of class 9.All the solutions of questions are created by future study point by a step by step way for helping the students to boost their preparations for the CBSE board exams.You can also study here NCERT solutions of science and maths from class 9 -12, sample papers, solutions of previous years question papers, tips for entrance exams of government jobs, carrier in online jobs.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
You can download pdf of NCERT solutions of class 9 maths chapter 8-Quadrilateral
pdf-NCERT Solutions of Class 9 Maths chapter 8-Quadrilateral
pdf of class 9 NCERT solutions of the chapter 7 -Triangles
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
CBSE Maths Class IX solutions of important questions of last years question papers
CBSE Class 9 maths assignment for SA-1
CBSE class 9 Notes on Lines, angles, and triangles
Addition, subtraction, and division of polynomials
Solutions of maths specific questions of mensuration
CBSE class 9 maths, midpoint theorem
NCERT Solutions of Class 9 Science : Chapter 1 to Chapter 15
NCERT Solutions Class 9 Maths Exercise 8.2 of chapter 8- Quadrilateral
Q1.ABCD is a quadrilateral in which P, Q, R, and S midpoints of the sides AB, BC, CD, and DA (see the given figure ).AC is a diagonal. Show that:
(i) SR ll AC, SR = 1/2(AC)
(ii) PQ = SR
(iii)PQRS is a parallelogram
Ans.
GIVEN: ABCD is a quadrilateral in which P,Q,R and S mid points of the sides AB,BC, CD and DA
TO PROVE:
(i) SR ll AC, SR = 1/2(AC)
(ii) PQ = SR
(iii)PQRS is a parallelogram
PROOF:
(i) In ΔADC, R is the mid point point of DC and S is the mid point of AD
According to mid point theorem the line segment joining the mid points of a triangle is parallel to third side and half of the third side in length.
SR ll AC
SR = 1/2(AC)
(ii) In ΔABC ,P is the mid point of AB and Q is the mid point of BC ,then using mid point theorem
PQ ll AC
PQ = 1/2(AC)…(i)
SR = 1/2(AC) …(ii)[proved above in (i)]
From equation (i) and (ii)
PQ = SR
(iii) According to mid point theorem,from the figure we have
SR ll AC….(i)
PQ ll AC….(ii)
From equation (i) and (ii) PQ ll SR
PQ = SR (proved above)
According to the theorem of the parallelogram, if one pair of opposite sides of a quadrilateral are equal and parallel, then the other pair of opposite sides is also parallel and equal.
PS ll QR and PS = QR
Therefore PQRS is a parallelogram, Hence proved.
How to choose your subjects after 10 or 12 pass
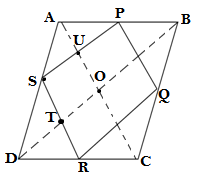
Q2.ABCD is a rhombus and P, Q, R, and S are midpoints of the sides AB, BC, CD, and DA respectively. Show that quadrilateral PQRS is a rectangle.
Ans.
GIVEN: ABCD is a rhombus and P,Q,R and S are midpoints of the sides AB, BC, CD, and DA
TO PROVE: PQRS is a rectangle.
PROOF: In ΔABD
PS∥BD (mid point theorem)
∴SU ∥ TO…..(i)
In ΔADC
SR∥AC (mid point theorem)
∴ST ∥ OU….(ii)
From equation (i) and equation (ii),we get that OUST is a parallogram
Therefore ∠ UST = ∠TOU (opposite angle of parallelogram)
∠TOU = 90°(diagonal of rhombus bisect each other at 90°)
∴∠ UST = 90°
Similarly ∠PQR = ∠QRS = ∠QPS =90°
Therefore PQRS is a rectangle, Hence proved
Q3.ABCD is a rectangle and P,Q,R and S are midpoints of the sides AB,BC,CD and DA respectively .Show that quadrilateral PQRS is a rhombus.
Ans.
GIVEN:ABCD is a rectangle P,Q,R and S are midpoints of the sides AB,BC,CD and DA respectively
TO PROVE: quadrilateral PQRS is a rhombus
PROOF:
In ΔABD, P is the mid point of AB and S is the mid point of AD
Therefore applying mid point theorem
PS∥BD
In ΔBDC, Q is the mid point of BC and R is the mid point of DC
Therefore applying mid point theorem
QR∥BD
In ΔADC, S is the mid point of AD and R is the mid point of DC
Therefore applying mid point theorem
SR∥AC
In ΔABC, P is the mid point of AB and Q is the mid point of BC
Therefore applying mid point theorem
PQ∥AC
AC = BD (diagonal of rectangle)
From equation (i), (ii),(iii) and (iv), we have
PQ = QR = SR = PS
Hence PQRS is a rhombus
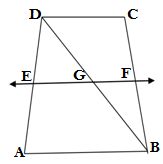
Q4. ABCD is a trapizium in which AB∥ DC, BD is a diagonal and E is the mid point of AD. A line is drawn through E parallel to AB intersecting BC at F(see the given figure). Show that F is the mid point of BC.
Ans.
GIVEN: AB∥ DC
E is the mid point of AD
EF∥ AB
TO PROVE:F is the mid point of BC
PROOF: Let EF intersects diagonal BD at G
In ΔABD
EF∥ AB
∴EG ∥ AB
According to converse of mid point theorem ,If E is the mid point of AD and EG ∥ AB, then G will also the mid point of BD
In ΔBDC
GF ∥ DC (DC∥ AB∥EF)
According to converse of mid point theorem ,If G is the mid point of BD and GF ∥ DC, then F will also the mid point of BC
Hence proved
NCERT Solutions Class 9 Maths Exercise 8.2 of chapter 8- Quadrilateral
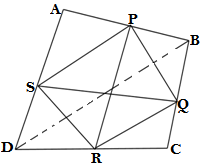
Q5. In a parallelogram ABCD, E and F are mid point of the sides AB and CD respectively (see the figure). Show that the line segments AF and EC trisect the diagonal BD.
Ans.
GIVEN:ABCD is a parallelogram
E is mid point of the side AB
F is mid point of the side CD
TO PROVE: DP = PQ = BQ
PROOF: In ABCD parallelogram
CF = DC/2….(i)(F is mid point of the side DC)
AE = AB/2(E is mid point of the side AB)
AB = DC (opposite sides of parallelogram )
AE = DC/2….(ii)
From the equations (i) and (ii)
CF = AE
CF ∥ AE
If a pair of opposite sides of a quadrilateral is equal and parallel then another pair of opposite sides is also equal and parallel
So. in AECF quadrilateral
AF ∥ CE
Therefore in ΔDQC,F is the mid point of DC
PF ∥ CQ ( since AF ∥ CE proved above)
According to converse of mid point theorem ,If F is the mid point of DC and PF ∥ CQ, then P will also the mid point of DQ.
∴DP = PQ….(i)
Similarly ,we can consider ΔAPB and can prove
PQ = BQ…..(ii)
From equation (i) and (ii)
DP = PQ = BQ
Hence proved
Please follow us on pintrest
Q6. Show that line segments joining the mid points of the opposite side of a quadrilateral bisect each other.
Ans.
GIVEN: ABCD is a quadrilateral
P ,Q,R and S are the mid points of the sides AB, BC, DC and AD respectively.
TO PROVE: PR and QS bisect each other
PROOF:
In ΔABD, P is the mid point of AB and S is the mid point of AD
Therefore applying mid point theorem
PS∥BD
n ΔBDC, Q is the mid point of BC and R is the mid point of DC
Therefore applying mid point theorem
QR∥BD
From (i) and (ii)
PS = QR
PS ∥ QR (since PS ∥ BD and QR ∥ BD)
If a pair of opposite sides of a quadrilateral is equal and parallel then another pair of opposite sides is also equal and parallel
Therefore SR = PQ , SR ∥ PQ
Now it is clear that PQRS is a parallelogram
Since diagonal of parallelogram bisect each other
Therefore PR and QS bisect each other, Hence proved
Q7. ABC is a triangle right angled at C. A line through the mid point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid point of AC
(ii) MD ⊥ AC
Ans.
GIVEN: ΔABC in which ∠C= 90°
M is mid point of hypotenuse AB
BC∥ MD
TO PROVE:
(i) D is the mid point of AC
According to converse of mid point theorem ,If M is the mid point of AB and BC∥ MD, then D will also the mid point of AC.
(ii) MD ⊥ AC
Since BC∥ MD (given)
∴∠MDC + ∠C = 180° (sum of co-interior angles)
∠MDC + 90°= 180°
∠MDC = 180° – 90° = 90°
Therefore MD ⊥ AC
In ΔAMD and ΔCMD ,we have
AD = CD [D is mid point of AC ,proved above in (i)]
DM = DM (common)
∠ADM = ∠CDM = 90° [proved above in (ii)]
ΔADM ≅ ΔCDM(SAS rule of congruency of triangles)
CM = MA (by CPCT)
Since, M is the mid point of AB
Therefore
Hence proved
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution