NCERT Solutions of Class 9 maths exercise 7.3 – Triangle
NCERT Solutions of Class 9 maths exercise 7.3 of chapter 7- Triangles are created by futurestudypoint.com for helping the class 9 students of CBSE. These NCERT solutions are the solutions of unsolved questions of exercise 7.3 of chapter 7- Triangles of class 9 Maths NCERT textbook. The questions of Exercise 7.3 -Triangle are based on the congruency of the triangle when the median of a triangle, and the perpendicular bisector of the triangle are given. All the questions are solved by a step-by-step method so that each student could clear the concept of each question.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Here in futurestudypoint.com,you can study all NCERT solutions of science and maths from class 9 – 12, science and maths special notes for the purpose of clearance of doubts among the students, our articles on government and other competitive entrance exams, carrier in online jobs .
NCERT Solutions of Class 9 Science : Chapter 1 to Chapter 15
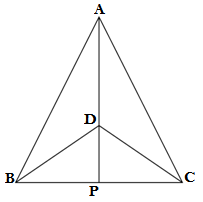
Q1. ΔABC and ΔDBC are two isosceles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ACD
(ii)ΔABP ≅ ACP
(iii)AP bisects ∠A and as well as ∠D
(iv) AP is the perpendicular bisector of BC
Ans.
GIVEN: ΔABC and ΔDBC are two isosceles with a common base BC
In which AB = AC and AD = DC
(i) TO PROVE: ΔABD ≅ ACD
PROOF:AB = AC (given)
BD = CD (given)
AD = AD (common)
ΔABD ≅ ACD (SSS rule)
Hence proved
(ii) TO PROVE:ΔABP ≅ ACP
PROOF: AB = AC (given)
AP = AP(common)
Since we have already proved ΔABD ≅ ACD
∴∠BAP = ∠PAC (By CPCT)
ΔABP ≅ ACP(SAS rule)
Hence proved
(iii TO PROVE: AP bisects ∠A and as well as ∠D
PROOF:In ΔDPB and ΔDPC
Since we have proved ΔABD ≅ ACD and ΔABP ≅ ACP
∴ BD = DC (By CPCT) and BP = PC (CPCT)
DP = DP (common)
ΔDPB ≅ΔDPC
∠DPB =∠DPC (By CPCT)…(i)
And it is already proved ΔABD ≅ ACD
∠BAD=∠DAC (By CPCT)….(*ii)
From (i) and (ii) it is clear that AP bisects ∠A and as well as ∠D
Hence proved
(iv) TO PROVE: AP is the perpendicular bisector of BC
PROOF: Since we have proved ΔABP ≅ ACP
Therefore ∠APB = ∠APC (By CPCT)
BP = PC(By CPCT)…..(i)
∠APB + ∠APC = 180°
∠APB +∠APB = 180°
2 ∠APB = 180°
∠APB = 90°
∴ AP ⊥ BC……(ii)
From (i) and (ii), it is cleared that AP is a perpendicular bisector of BC
Hence proved
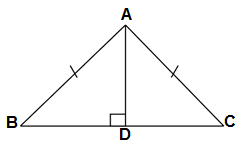
Q2.AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that (i) AD bisects BC (ii) AD bisects ∠A.
Ans.
GIVEN: An isosceles triangle ΔABC in which AB = AC
AD is the altitude of the isosceles triangle
∴ ∠ADC = ∠ADB = 90°
TO PROVE: (i) AD bisects BC
In ΔABD and ΔACD
AD = AD (common)
AB = AC (given)
∠ADC = ∠ADB = 90° (AD ⊥ BC)
ΔABD ≅ ΔACD(RHS rule)
BD = DC (By CPCT)
Hence AD bisects BC
(ii) TO PROVE: AD bisects ∠A.
Since we have proved ΔABD ≅ ΔACD
∴∠BAD = ∠DAC (By CPCT)
Therefore AD bisects ∠A
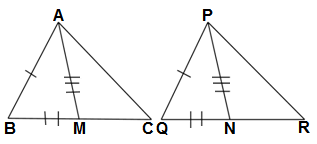
Q3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR see the given figure. Show that.
(i) ΔABM ≅Δ PQN
(ii)ΔABC ≅ ΔPQR
Ans.
GIVEN: In ΔABC and ΔPQR
AB = PQ
BC = QR
AM = PN
TO PROVE: (i) ΔABM ≅Δ PQN
PROOF: AB = PQ (given)
AM = PN (given)
BC = QR (given)
Since AM is the median of the triangle ΔABC and PN is the median of the triangle ΔPQR
∴BC/2 = QR/2
BM = QN
ΔABM ≅Δ PQN (SSS rule)
Hence proved
TO PROVE (ii)ΔABC ≅ ΔPQR
PROOF: Since we have already proved ΔABM ≅Δ PQN
∴∠ABM = ∠PQN (by CPCT)
AB = PQ (given)
BC = QR(given)
ΔABM ≅Δ PQN (SAS rule)
Hence proved
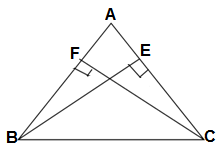
Q4. BE and CF are two equal altitudes of a triangle ABC. Using the RHS congruence rule, prove that the triangle ABC is isosceles.
Ans.
GIVEN: In ΔABC, in which two altitudes BE and CF are equal
BE = CF
∠CFB = ∠CEB = 90°
TO PROVE: triangle ABC is isosceles
In ΔCFB and ΔBEC
The hypotenuse of both right triangles is common
BC = BC (common)
∠CFB = ∠CEB = 90°(BE and CF are altitudes of both triangles)
BE = CF (equal)
ΔΔCFB≅ ΔBEC (RHS rule)
∠B = ∠C (by CPCT)
AB = AC (opposite sides of equal triangles)
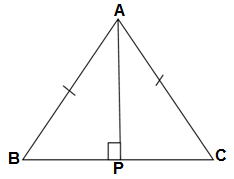
Q5. ABC is an isoscles triangle with AB = AC . Draw AP⊥ BC to show that ∠B = ∠C.
Ans.
GIVEN: In triangle ABP and triangle ACP
AB = AC
∠APB = ∠APC = 90° (AP ⊥ BC)
TO PROVE:∠B = ∠C
PROOF: In ΔABP and ΔACP
AB = AC (given)
AP = AP (common)
∠APB = ∠APC = 90°(given)
ΔABP ≅ ΔACP (RHS rule)
∠B = ∠C (by CPCT)
Hence proved
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution