Addition of Vectors: Class 11 Physics Chapter 4 CBSE

Triangular Law of Vector Addition: Following the rule of parallel shifting, draw one vector and then draw another vector such that the head of one vector is joined to the tail of another vector, thereafter joining the tail of the former vector to the head of the later vector, we get the resultant vector of both vectors which is the addition of the vectors.

As an example, a displacement of 3 m east and a displacement of 4 m north, then find the addition of the vector

Let the vector = 3 m east and = 4 m north then their addition is

Hence the resultant of both vectors is 5 m northwest,so there are specific rule for vector addition,we can’t add them like the scaler quantity means the resultant can’t be 3 +4 =7

What is the resultant of two vectors when the angles between them is other than 90°

Let there be two vectors    and   then their addition is represented as follows

The resultant R of both vectors is given as

The vector sum of both vectors is not a simple addition,the method mentioned above is head to tail method,apart from that there are other methods of solving vector addition.

The resultant of head to tail method is applicable when both vectors are in a same line or perpendicular to each other,so when both vectors have a certain angle θ between them then their resultant vecor is evaluated by parallelogram rule of vector addition.

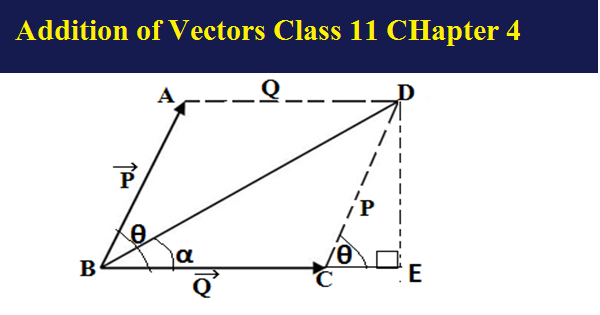
Parallelogram Law of Vectors addition: In this method, two vectors are drawn tail to tail as they are adjacent sides of a parallelogram and then geometrically completing the parallelogram,then the diagonal obtained by joining the vertex of both vectors to the opposite vertex of the parallelogram shows their resultant.

Draw two vectors P and Q such that they join each other tail to tail

Complete the parallelogram ABCD, then draw a DE⊥CE

The sides AD =Q=AB,DC =P=AB shows magnitudes of the vectors

BD  will show the resultant of the vectors

Let both vectors have angle θ between them and the resultant forms an angle of α between them and the magnitude of the resultant vector is R

Considering the right ΔBDE

∠ABC = ∠DCE=θ

BD² = BE² + DE²

R² =(BC+CE)² +DE²

R² = BC² +CE² +2BC.CE + DE²

R² = Q² + CE²+ 2Q.CE + DE²…….(i)

Let us find the value of CE and DE

Considering the triangle ΔDCE

cos θ =CE/DC and sinθ = DE/DC

CE = DCcos θ =Pcos θ …..(ii) and DE =DCsin θ= Psin θ …..(iii)

Putting the value of CE and DE in equation (i)

R² = Q² + (Pcos θ)²+ 2Q.Pcos θ + (Psin θ )²

R² = Q² + P²cos² θ+ 2Q.Pcos θ + P²sin ²θ

R² = Q² + P²(cos² θ+sin ²θ)+2Q.Pcos θ

R² = Q² + P²+2PQcos θ 

The above equation is used for determining the magnitude of the resultant of two vectors

Now

tanα =DE/BE

BE =BC +CE =Q+ Pcosθ

From equation (ii) and (iii)

tanα = Psinθ/(Q+ Pcosθ)

This equation is used to determine the direction of resultant

Don’t forget to write a comment , subscribe us for the posts related to your study

Circular Motion: Angular velocity and angular displacement

Electronic Configuration of s,p and d orbitals

Atomic Radius Class 11 Chemistry Chapter 3 Periodicity in Properties

Why does Rainbow looks like a Bow?

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT Solutions for Class 11 Physics

Chapter 1- Physical World

chapter 3-Motion in a Straight Line

NCERT Solutions for Class 11 Chemistry

Chapter 1-Some basic concepts of chemistry

Chapter 2- Structure of Atom

NCERT Solutions for Class 11 Biology

Chapter 1 -Living World

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution