Class 10 CBSE Maths Solutions of 3 and 4 Marks Questions Asked in the Last Years Exam-Part 1.

Class 10 CBSE Maths Solutions of 3 and 4 Marks Questions Asked in the Last Years Exam-Part 1 are very important to study for achieving excellent marks since among all the questions existing in the question papers 60-65 % marks of the questions are contributed by the questions of 3-4 marks.Studying 3-4 marks questions will automatically cover your preparations for other remaining questions of 1 and 2 marks,so you can now understand the importance of 3-4 marks questions which are responsible for excellent marks or achieving A + grade in mathematics.

Class 10 CBSE Maths Solutions of 3 and 4 Marks Questions Asked in the Last Years Exam-Part 1.

Q1.If the sum of first four terms of an AP is 40 and that of first 14 terms is 280 .Find the sum of its first n terms.

Ans. The sum of n terms of an AP is given by

${\color{DarkBlue} \boldsymbol{S_{n}=\frac{n}{2}\left [ 2a+\left ( n-1 \right )d \right ]}}$

Where ‘a’ is the first term and ‘d’ is the common difference of the given AP.

According to first condition n = 4, sum of 4 terms = 40

${\color{DarkBlue} \boldsymbol{S_{4}=\frac{4}{2}\left [ 2a+\left ( 4-1 \right )d \right ]}}$

40= 2(2a + 3d)

2a + 3d = 20……………(i)

According to second condition n = 14 and sum of 14 terms=280

${\color{DarkBlue} \boldsymbol{280=\frac{14}{2}\left [ 2a+\left ( 14-1 \right )d \right ]}}$

2a + 13d = 40………….(ii)

Subtracting ( i) from (ii) we get

10d = 20

d = 2

Substituting d= 2 in equation (i) or (ii),we get a = 7

Putting a =7 and d = 2 in sum formula of the AP,we will get sum of n terms

${\color{DarkBlue} \boldsymbol{S_{n}=\frac{n}{2}\left [ 2\times 7+\left ( n-1 \right )\times 2 \right ]}}$

${\color{DarkBlue} \boldsymbol{S_{n }=n\left ( n+6 \right )=n^{2}+6n}}$

Hence the sum of n terms will be n² + 6n

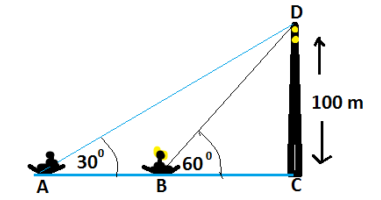
Q2.A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60º to 30º respectively. Find the speed of boat in meters per minute.(√3 =1.732)

Ans.

To find the speed of boat we are needed to find the distance AB traveled by boat in 2 minutes

From the figure AB = AC – BC, Let’s find AC and BC

In ΔADC and ΔBDC, we have

${\color{DarkBlue} \boldsymbol{tan30^{\circ}=\frac{DC}{AC} }}$

${\color{DarkBlue} \boldsymbol{AC =100\sqrt{3}}}$

${\color{DarkBlue} \boldsymbol{tan60^{\circ}=\frac{DC}{BC} }}$

${\color{DarkBlue} \boldsymbol{BC=\frac{100}{\sqrt{3}}}}$

${\color{DarkBlue} \boldsymbol{\therefore AB=100\sqrt{3}-\frac{100}{\sqrt{3}}=\frac{300-100}{\sqrt{3}}=\frac{200}{\sqrt{3}}}}$

${\color{DarkBlue} \mathbf{Speed \; of\; boat=\frac{AB}{2}=\frac{200}{2\sqrt{3}}}}$

${\color{DarkBlue} \mathbf{Speed \; of\; boat=\frac{AB}{2}=\frac{200}{2\sqrt{3}}=\frac{100}{\sqrt{3}}}}$

${\color{DarkBlue} \boldsymbol{=\frac{100\sqrt{3}}{\sqrt{3}\times \sqrt{3}}=\frac{100\sqrt{3}}{3}}}$

${\color{DarkBlue} \boldsymbol{=\frac{100\times 1.732}{3}=\frac{173.2}{3}=57.73}}$

Therefore the speed of boat will be 57.73 meters/minute

Q3.A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm². The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it.

Ans.

Volume of bucket = 12308.8 cm.cube, let the height of the bucket = h

${\color{DarkBlue} \boldsymbol{r_{1}=20\; cm,\; r_{2}=12cm}}$

${\color{DarkBlue} \mathbf{V=\frac{\Pi h}{3}\left ( r_{1} ^{2}+r_{2}^{2}+r_{1}r_{2}\right )}}$

${\color{DarkBlue} \boldsymbol{\frac{\Pi h}{3}\left [ r_{1}^{2} +r_{2}^{2}+r_{1}r_{2}\right ]=12308.8}}$

${\color{DarkBlue} \boldsymbol{\frac{22 h}{21}\left [ 20^{2} +12^{2}+12\times 20\right ]=12308.8}}$

${\color{DarkBlue} \boldsymbol{\frac{22 h}{21}\left [ 400 +144+240\right ]=12308.8}}$

${\color{DarkBlue} \boldsymbol{\frac{22 \times 784h}{21}=12308.8}}$

${\color{DarkBlue} \boldsymbol{h=12308.8\times \frac{21}{22\times 784}}}$

h = 15

Therefore height of the bucket =15 cm

S-Surface area of bucket

${\color{DarkBlue} \boldsymbol{S=\Pi r_{2}^{2}+\Pi \left ( r_{1}+r_{2} \right )l}}$

l-slant height

${\color{DarkBlue} \boldsymbol{l=\sqrt{h^{2}+\left ( r_{1} -r_{2}\right )^{2}}}}$

${\color{DarkBlue} \boldsymbol{=\sqrt{15^{2}+\left ( 20 -12\right )^{2}}}}$

${\color{DarkBlue} \boldsymbol{=\sqrt{225+64}=\sqrt{289}=17}}$

${\color{DarkBlue} \boldsymbol{S =\frac{22}{7}\times 12^{2}+\frac{22}{7}\left ( 12+20 \right )\times 17}}$

${\color{DarkBlue} \boldsymbol{=\frac{22}{7}\left ( 144+544 \right )}}$

${\color{DarkBlue} \boldsymbol{=\frac{15136}{7}}}$

= 2162.29

Therefore the height of the bucket is 17 cm and the area of metal sheet used in making the bucket is 2162.29 cm².

Study most important questions for your CBSE board exam 2020

Reflection refraction dispersion and scattering of light

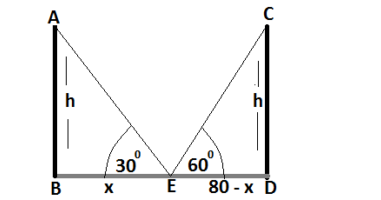
Q4.Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles.

Ans.

Let two poles AB and CD of the height h are the two poles standing opposite each other on either side of the road and the distance of AB from a point E on the road is x meter and of CD is 80 –x.

In ΔABE and ΔDCE we have

${\color{DarkBlue} \boldsymbol{tan30^{\circ}=\frac{AB}{BE}=\frac{h}{x},tan60^{\circ}=\frac{DC}{CE}=\frac{h}{80-x}}}$

${\color{DarkBlue} \boldsymbol{\frac{1}{\sqrt{3}}=\frac{h}{x},\; \sqrt{3}=\frac{h}{80-x}}}$

${\color{DarkBlue} \boldsymbol{x=h\sqrt{3}\;......\left ( i \right ),\; \sqrt{3}\left ( 80-x \right )=h.....\left ( ii \right )}}$

Substituting x =h√3 in (ii)

√3(80– h√3) =h

80√3 – 3h = h

4h =80√3

h = 20√3

Putting the value of h in equation (i)

x = 20√3 × √3 = 20 × 3 = 60

Therefore the height of both poles is 20√3 m and the distances of poles from the point on the road are 60 m and 80–60 = 20 m.

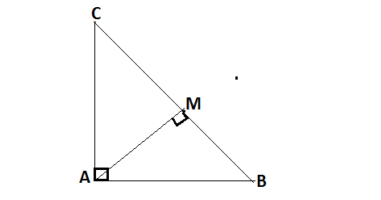
Q5.Prove that in a right-angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.

Ans

GIVEN. A right ΔABC

TO PROVE. BC² = AB² + AC²

CONSTRUCTION. Drawing AM ⊥ BC

PROOF. Considering the ΔABC and ΔABM

∠B = ∠B (Common)

∠BAC = ∠AMB (AM ⊥ BC)

ΔABC ∼ ΔMBA

According to rule of similarity

${\color{DarkBlue} \mathbf{\frac{AB}{BM}=\frac{BC}{AB}=\frac{AC}{AM}}}$

We are required

${\color{DarkBlue} \mathbf{\frac{AB}{BM}=\frac{BC}{AB}}}$

AB² = BC.BM………….(i)

Considering ΔABC and ΔAMC

∠C = ∠C (Common)

∠BAC = ∠AMC (AM ⊥ BC)

ΔABC ∼ ΔMAC (AA rule)

${\color{DarkBlue} \boldsymbol{\frac{AB}{AM}=\frac{BC}{AC}=\frac{AC}{CM}}}$

We are required

${\color{DarkBlue} \boldsymbol{\frac{BC}{AC}=\frac{AC}{CM}}}$

AC² = BC.CM………..(ii)

Adding both equations (i) and (ii)

AB² + AC² = BC.BM + BC.CM

AB² + AC² = BC (BM + CM)

AB² + AC² = BC.BC ( BM + CM = BC)

BC² = AB² + AC², Hence Proved

Therefore the square of the hypotenuse is equal to the sum of squares of the other two sides in a right triangle.

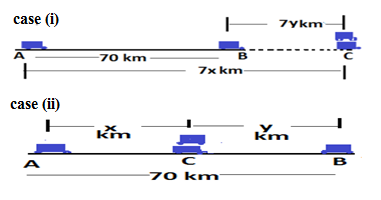
Q6.There are two points on highway A,B. They are 70 km apart. An auto starts from A and another auto starts from B simultaneously. If they travel in the same direction, they meet in 7 hours, but if they travel towards each other they meet in 1 hour. Find how fast the two autos are.

Ans. Let one of the autos starts from A with a speed of x km/hr and other starts from point B with a speed of y km/hr.

The case when they move in the same direction, they meet after 7 hours,so the distance traveled by auto which starts from A is 7x km and the distance traveled by another auto is 7y km.

From the fig. above case (i)

7x – 7y = 70

x – y = 10…………(i)

The case when both the auto moves in the opposite direction, they meet after one hour, the distances traveled by auto which starts from A is x km and by the auto from B is y km.

From the fig. above case (ii) we have

x + y = 70………………..(ii)

Adding (i) and (ii) we have

2x = 80

x = 40

Putting x = 40 in equation (ii)

y = 70 – 40 = 30

Hence the speed of the auto starts from A is 40 km/hr and which starts from B is 30 km/hr

Class 10 CBSE Maths Solutions of 3 and 4 Marks Questions Asked in the Last Years Exam

Class 10 maths Important Questions of 3-4 marks(Part-II))

Class 10 Important maths questions of 3-4 marks-(Part-lll)

Solutions of half yearly class 10 maths question paper-2020

Solutions of class 10 maths question paper of 2019 CBSE Board

Solutions of class 10 maths question paper 2020 CBSE Board

NCERT Solutions of all chapters of Maths for Class 10 from Chapters 1 to 15

NCERT Solutions Class 10 Science from chapter 1 to 16

Science and Maths NCERT solutions for Class 9 ,10 and 11 classes

Study notes of Maths and Science NCERT and CBSE from class 9 to 12

Important maths notes

Tricks – How to write linear equations

Tricks- How to solve question from algebraic equations

Three ways of solving quadratic equation

Mean, Mode and Median

Solutions- Specific questions of mensuration

Finding the roots of the polynomial by Complete square method

Technics – Achieving 100% marks in Maths

Class X Most important questions of Maths

Solutions-class X Most important questions of 3-4 marks

Solutions of the qustions based on Expressions and Equations

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals