NCERT Solutions Of Chapter 6 Exercise 6.3

NCERT solutions of chapter 6 exercise 6.3 is going to help all the maths students of class 12,in this exercise 6.3 of the maths chapter class 12 -Application of Derivatives you will learn solutions of the questions related to the slope of the curve. All questions are explained by an expert of the subject as per the CBSE norms. NCERT Solutions of the exercise 6.3 Application of Derivatives will give an idea to all students about the concept and the way of solving the questions of exercise 6.3 of chapter 6 which is required to solve all the questions of Application of Derivatives in the Class 12 CBSE Board exam.

You can also study

Exercise 6.1 – Application of Derivatives

Exercise 6.2 – Application of Derivatives

Exercise 6.3 – Application of Derivatives

Exercise 6.4- Application of Derivatives

NCERT Solutions Of Chapter 6 Exercise 6.3

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q1.Find the slope of the tangent to the curve at x = 4.

Ans. The slope of the tangent to the curve   is

If x = 4, the slope =

Q2.Find the slope of the tangent to the curve 

Ans. We are given the equation of the curve

The slope of the given curve is the differentiation of y with respect to x as follows

If x = 10, the slope =

Q3.Find the slope of the tangent to the curve y = x³ – x + 1 at the point whose x-coordinate is 2.

Ans. The slope of the tangent to the curve

  is

y = x³ – x + 1

= 3x²- 1

Slope of the curve at x = 2

3 × 2²- 1

12 -1 = 11

Q4.Find the slope of the tangent to the curve y = x³ – 3x + 2 at the point whose x-coordinate is 3

Ans. We are given the curve y = x³ – 3x + 2

y = x³ – 3x + 2

= 3x² – 3

The slope of the curve at x = 3

3 × 3² – 3 = 27 – 3 = 24

Q5.Find slope of the normal to the curve x = a cos³θ, y = a sin³θ at θ = π/4.

Ans. We are given

x = a cos³θ, y = a sin³θ

The slope of the curve is = -1

Let the slope of the normal to the curve = m

We know the relation

the slope of the curve × m = -1

-1 × m = -1

m = 1

Q6. Find the slope of the normal to the curve x = 1 – a sinθ, y = b cos”θ at θ = π/2.

Ans. We are given the curve

x = 1 – a sinθ,        y = b cos”θ

The slope of the given curve is

The slope of the curve at θ = π/2

So, slope of the curve, m = 2b/a

Let slope of the normal to the curve is = M

We have

Hence normal to the given curve is = -a/2b

NCERT Solutions Of Chapter 6 Exercise 6.3

Q7. Find points at which the tangent to the curve y = x³ – 3x² – 9x + 7 is parallel to the x-axis.

Ans. The given curve is

y = x³ – 3x² – 9x + 7

Slope of the tangent dy/dx is evaluated as follows

Since the tangent to the curve is parallel x-axis

The equation of x-axis is

y = 0

It is given to us that   the tangent to the curve is parallel to each other

So, 3x² – 6x – 9 = 0

x² – 2x – 3 = 0

x² – 3x + x – 3 = 0

x( x – 3) + ( x – 3) = 0

( x – 3)(x + 1) = 0

x = 3, -1

Hence at x = 3, -1 the tangent to the curve is parallel to x-axis

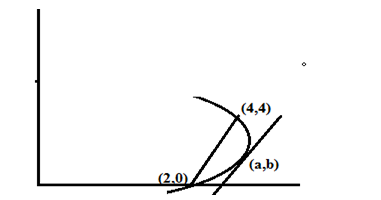
Q8.Find a point on the curve y = (x – 2)² at which the tangent is parallel to the chord joining the points (2,0) and (4,4).

Ans.

 

 

 

Calculating the slope of tagent to the given curve, y = (x – 2)²

y = (x – 2)²

Slope of the chord joining the points (2,0) and (4,4) = m

We are given that the tangent is parallel to the given chord of the curve, so their slopes must be equal

2(x – 2) = 2

x = 3

Putting this value of x in the equation of the curve

y = (3 – 2)² = 1

Therefore the point on the given curve is (3,1) in which tangent is parallel to the given chord.

Q9. Find the point on the curve y = x³ – 11x + 5 at which the tangent is  y = x -11.

Ans. The given curve is

y = x³ – 11x + 5

Finding its slope as following

= 3x² – 11

The slope of the given tangent y = x -11 is calculated as follows

The slope of the curve = Slope of the tangent

3x² – 11 = 1

x = ±2

If x = 2, then y = 2 – 11 = -9, if x = -2, then y= -2 -11 = -13

(-2,-13) does’t satisfy the equation of the curve so it does’t lie on the curve

The point (2, -9) satisfy the equation of the curve so the given tangent on the curve is at (2, -9)

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT Solutions for Class 11 Physics

Chapter 1- Physical World

chapter 3-Motion in a Straight Line

NCERT Solutions for Class 11 Chemistry

Chapter 1-Some basic concepts of chemistry

Chapter 2- Structure of Atom

NCERT Solutions for Class 11 Biology

Chapter 1 -Living World

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution