Quantum Numbers and Orbitals Class 11 Chemistry
The groundwork for our understanding of atomic structure was laid by the pioneering work of German scientist Niels Bohr. He introduced the quantum theory of atomic structure, proposing that electrons orbit the nucleus in specific circular paths termed energy levels or shells. Each of these shells, denoted by letters such as K, L, M, N, etc., can hold a maximum number of electrons given by the formula 2n², where n is a natural number. Bohr postulated that electrons within these shells remain stable without emitting energy.
Bohr’s concept introduced the first quantum number, n, which signifies the principal quantum number of an atom, providing insights into the electron’s shell. However, further developments by Erwin Schrödinger expanded upon Bohr’s model. Schrödinger proposed that electrons do not orbit the nucleus akin to planets around the sun; instead, they occupy regions known as subshells. These subshells are defined by the atom’s angular momentum and are represented by azimuthal quantum numbers.
In refining the atomic model, Schrödinger introduced additional quantum numbers. The second quantum number describes the spatial orientation of the subshell, distinguishing regions along the x, y, and z axes. These regions, termed orbitals, are where electrons are likely to be found. Schrödinger termed this quantum number the magnetic quantum number because external magnetic fields influence the splitting of subshells into orbitals, affecting the distribution of electrons. This refinement of the atomic model provided a more nuanced understanding of electron behavior within atoms.
Quantum numbers are the index number that are used to identify the position ,energy and momentum of the electron in an atom.These quantum numbers are of four types.
(i) Principal quantum number(n)
(2)Azimuthal quantum number(l)
(3)Magnetic quantum number(M)
(4)Spin quantum number(s)
Atomic radius: Periodicity in Properties of the elements
Principal Quantum Number:
(i)It is represented by n .
(ii)Principal quantum number was discovered by Neil’s Bohr.
(iii)Each shell is represented by a principal quantum number, where n=1,2,3……∞ which corresponds to shell K,L, M,N…..
(iv)The number of maximum electrons accommodated in each shell is given by the expression 2n²
As an example the number of electrons in K,L,M,N …are given as
Number of electrons in K=2n²=2×1²=2
Number of electrons in L=2n²=2×2²=8
Number of electrons in M=2n²=2×3²=18
…………….And so on
(v) With the increase of the principal quantum number the size and energy of shell increases.
(vi)Principal quantum number also decides the radius of the shell,if we know the principal quantum number of an electron the we can calculate radius of the shell in which electron is moving from the following formula.
Radius of the shell = 0.529n²/z,where n is the principal quantum number and z is the atomic number of the atom.
Energy of the shell=-13.6z²/n²
(2)Azimuthal quantum number(l)
(i) Azimuthal quantum number is represented by l and it shows the angular momentum of the electron.
(ii) Azimuthal quantum number gives information about the subshell.
(iii)The value of l is determined by the expression n -1,where n is the principal quantum number
(iv)The value of l gives the shape of the shell.
The number of subshells = 0 to n-1
As an example if principal quantum number is 4
l=0,1,2,3
The name of these subshells are given by the name s,p,d and f
l=0(s),l=1(p),l=2(d),l=3(f)
The number of shells = The number of subshells
Way of writing the electronic configuration
If principal quantum number,n=1 then l = 0
A subshell is designated as →1s(where 1 is the principal quantum number and s is the subshell)
Different subshell are designated by first writting the principal quantum number followed by subshell
For n =2, l=0,1
Subshells designated as l=0(2s),l=1(2p)
For n=3,l=0,1,2
Subshells designated as l=0(3s),l=1(3p),l=2(3d)
For n=4,l=0,1,2,3
Subshells designated as l=0(4s),l=1(4p),l=2(4d),l=3(4f)
Electronic capacity of the subshells
First Shell ,n =1(k) have capacity of 2 electrons
For n =1,there is one subshell (i,e l=0) therefore s subshell accomodates 2 electrons
For n =2, the second shell capacity is of 8 electrons, there are two subshells (i,e l=0,1) corresponding to two subshells(i.e s and p), s subshell accommodates 2 electrons, and rest 6 electrons will be accommodated in p subshell.
For n =3, the third shell capacity is of 18 electrons, there are three subshells (i,e l=0,1,2) corresponding to three subshells(i.e s , p and d), s subshell accommodates 2 electrons,p subshell accommodates 6 electrons and rest 10 electrons will be accommodated by d subshell.
For n =4, the fourth shell capacity is of 32 electrons, there are four subshells (i,e l=0,1,2,3) corresponding to four subshells(i.e s , p ,d and f) , s subshell accommodates 2 electrons,p subshell accommodates 6 electrons,d subshells accommodates 10 electrons and rest 14 electrons will be accommodated by f subshell.
Magnetic Quantum Number:
(i) Magnetic quantum number is shown by m.
(ii)Magnetic quantum number gives the number of orbitals and spatial orientation with respect to the coordinate axis.
(iii)Orbitals are the regions where the probability of finding electrons is maximum.
(iv)For any subshell,m has 2l+1 values which correspond to no. of orbitals.
(v)For every value of l ,the value of m are -l to l.
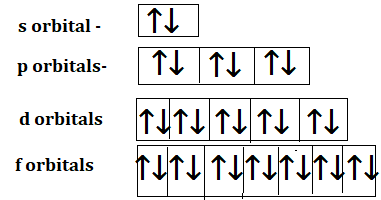
The number of orbitals in each subshell.
| Subshell(l) | The number of orbitals(2l+1) | Value of orbital(m) |
| s(i.e l=0) | 1 | 0 |
| p(i,e l=1) | 3 | -1,0,1 |
| d(i.e l=2) | 5 | -2,-1,0,1,2 |
| f(i.e l=3) | 7 | -3,-2,-1,0,1,2,3 |
Name of the orbitals:
The orbital (0) is named s orbital(since value of l is equal to the value of m)
The orbitals -1,0,1 are named Px,pyand pz
The orbitals -2,-1,0,1,2 are named Pxy,pyz ,pzx,Px²y² and pz²
Every orbital has a tendency of holding 2 electrons
Therefore s ,p,d and f orbitals will have 2,6,10 and 14 electrons.
Note: Students not needed to confuse s,p,d and f are subshells but when we talk about orbitals we consider 1,3,5 and 7 orbitals of s,p,d and f respectively.
Spin Quantum Number:
(i)Spin quantum number denoted by ‘s’
(ii)It shows the direction of spin of the electron.
(iii)An electron rotates about its own axis clockwise or anty clockwise.
(iv)The value of spin quantum number are denoted by +1/2 and -1/2.
Distribution of electrons in the orbitals
You can compensate us
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT Solutions for Class 11 Physics
chapter 3-Motion in a Straight Line
NCERT Solutions for Class 11 Chemistry
Chapter 1-Some basic concepts of chemistry
NCERT Solutions for Class 11 Biology
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution