Class 10 Maths NCERT Solutions of Chapter 10 Circle
NCERT Solutions For Class 10 Maths Chapter 10 Circle: NCERT Solutions For Class 10 Maths Chapter 10 Circle is one of the most important study inputs for your CBSE Board exams. This blog brings the Class 10 Maths NCERT Solutions of Chapter 10 Circle to get ready for board exams 2022-23. Solutions to every one of the unsolved questions of Class 10 NCERT Maths Chapter 10 are given here with suitable answers that offer you an idea to display how to solve maths questions in the most ideal manner in the exam. These NCERT Solutions of Maths Class 10 Chapter 10 Circle are created by an expert of Maths who has 20 years of experience in teaching Maths subjects to Class 9,10,11 and 12 .
Importance of NCERT Solutions For Class 10 Maths Chapter 10 Circle
Maths NCERT solutions for class 10 are the most valuable study inputs for achieving excellent marks in CBSE board exams, therefore all students are required to repeat NCERT solutions of maths cyclically. For achieving excellence in maths of class 10, 60-70 % contribution goes to NCERT solutions and the rest 30-40 % credit goes to the study of last year’s maths unsolved or solved question papers. In studying maths as much as you practice you learn more and more.
Download PDF-NCERT Solutions For Class 10 Maths Chapter 10 Circle
You can download a free PDF of NCERT Solutions For Class 10 Maths Chapter 10 Circle for studying it when you are offline, the link for downloading NCERT Solutions For Class 10 Maths Chapter 10 Circle is given below.
Download PDF-NCERT Solutions For Class 10 Maths Chapter 10 Circle
Class 10 Most Important Questions of Chapter 10 Circle
You can study the Most Important Questions of Chapter 10 Circle from the following link
Class 10 Most Important Questions on Chapter 10 -Circle
Class 10 Maths NCERT Solutions of Chapter 10 Circle
Exercise 10.1
Q1. How many tangents can a circle have?
Ans.A circle has infinite points and through each point a tangents can be drawn so a circle can have infinite tangents.
Q2.Fill in the blanks:
(i)A tangent to a circle intersects it in ……..point(s)
(ii)A line intersecting a circle in two points is called a ……….
(iii)A circle can have ………..parallel tangents at the most.
(iv)The common point of a tangent to a circle and the circle is called…….
Ans. (i) A tangent to a circle intersects it in one point.
(ii)A line intersecting a circle in two points is called a secant.
(iii)A circle can have two parallel tangents at the most.
(iv)The common point of a tangent to a circle and the circle is called the contact point.
Class 10 Maths Chapter 10 Circles NCERT Solutions Video One Shot, please be one of the our subscribers
Q3.A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A)12 cm (B)13 cm (C)8.5 cm (D) √(119) cm
Ans.
As we know OP⊥ PQ, because P is the contact point of the circle , PQ is the tangent on the circle and OP is the radius of circle.
∆OPQ is the right triangle
So, OQ² = OP² + PQ²
PQ ² = OQ² – OP²
PQ ² = 12² -5²
PQ² = 144 – 25 =119
PQ =√119
Hence the length of PQ is√119 cm
Class 10 Maths NCERT Solutions of Chapter 10 Circle
Exercise 10.2
In question number 1 to 3, choose the correct option and give justification.
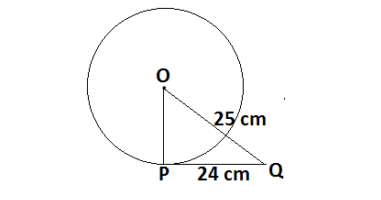
Q1.From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the center is 25 cm. The radius of the circle is.
(A) 7 cm (B)12 cm
(C)15 cm (D)24.5
Ans.
Let O is the centre of circle ,we are given that OQ = 25 cm, PQ = 24 cm
According to theorem OP ⊥ PQ, where OP is the radius and PQ is the tangent
Therefore ΔOPQ is the right triangle
Applying Pythagoras theorem
OQ² = PQ² + OP²
OP² = OQ² – PQ²
OP² = 25² – 24²
OP² = 625 – 576
OP² = 49
OP = 7
Therefore the length of the radius OP is 7 cm, so (A) is the right option.
Q2.In the given fig. if TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110º then ∠PTQ is equal to
(A) 60º (B)70º
(C)80 º (D)90º
Ans.
As we are given TP and TQ are tangents of the circle ,therefore P and Q will be contact points of tangents.
O is the centre of circle , therefore OP and OQ will be the radii of the given circle
∵OP⊥ TP and OQ ⊥ TQ ( The radius is perpendicular to the tangent)
∴∠OQT = 90º and ∠ OPT = 90º
∠POQ + ∠PTQ + ∠OQT + ∠ OPT = 360º (Angle sum property of quadrilateral)
110º + ∠PTQ + 90º + 90º = 360º
∠PTQ = 360º – 290º
∠PTQ = 70º
Therefore right option is (B).
Q3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80º then ∠POA is equal to
(A) 50º (B) 60º (C) 70º (D) 80º
Ans.
∠PAO = ∠PBO = 90º ( The radius is perpendicular to the tangent)
∠PAO + ∠PBO + ∠AOB + ∠APB = 360º (Angle sum property of quadrilateral)
90º + 90º + 80º +∠AOB = 360º
∠AOB = 360º – 260º
∠AOB = 100º
Considering ΔPOA and ΔPOB
OP = OP (Common)
OA = OB (Radii of same circle)
∠PAO = ∠PBO = 90º ( The radius is perpendicular to the tangent)
ΔPOA ≅ ΔPOB (RHS rule )
∠POA = ∠POB (By CPCT)
∠POA +∠POB = 100º
2∠POA = 100º
∠POA = 50º
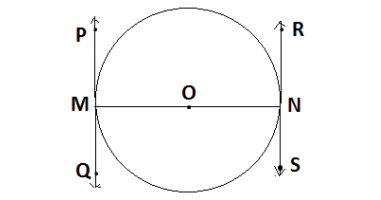
Q4. Prove that the tangents drawn at the ends of diameter of a circle are parallel to each other.
Ans. Let PQ and RS are the tangents drawn on both the ends of the diameter MN
MO and NO are the radii of the circle
PM ⊥ MO and RN ⊥ NO ( Radius is perpendicular to the tangent)
∴∠PMO = 90º and ∠ RNO = 90º
∠PMO + ∠ RNO =90º + 90º = 180º
Since the angles, ∠PMO and ∠ RNO are co-interior angles, MN transversal
Here the sum of co-interior angles is 180º, therefore RS ∥ PQ
Q5. Prove that perpendicular at the point of contact to the tangent to a circle passes through the centre.
Ans.
Let PQ is the tangent to a circle with centre O where T is the contact point of the tangent
Let TR ⊥ PQ , doesn’t pass through the centre O
∠OTQ = 90º (The angle between tangent and radius)
∠RTQ = 90º(We have supposed)
∠OTQ = ∠RTQ
R and O coincide to each other, therefore TR must have to pass through the centre of the circle.
Q6. The length of tangent AB from a point A at a distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Ans.
Let B is the contact point and AB is the tangent
∠ABO = 90º (Radius OB⊥ AB)
∴ABO is right triangle
Therefore the radius of the circle will be = 3 cm
Class 10 Maths NCERT Solutions of Chapter 10 Circle
Q7.Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Ans.
Let AB is the chord of the larger circle which touches smaller circle at C
OC ⊥ AB (The radius is perpendicular to the tangent)
ΔOCB will be a right triangle
BC² = OB² – OC²
BC² = 5² – 3²= 25 – 9 = 16
BC = 4
AB = 2 × BC (Perpendicular from centre to chord bisects the chord)
AB = 2 × 4 = 8
Therefore the length of the chord which touches smaller circle is 8 cm.
Click the link below and make your preparation easy
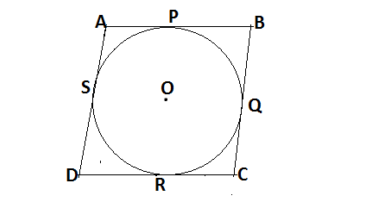
Q8. A quadrilateral is drawn to circumscribe a circle (see fig.) . Prove that AB + CD = AD + BC
Ans.
Let the circle touches the quadrilateral at P,Q,R and S points
Applying the theorem that tangent from an external point to the circle are equal
From the fig.we have
Hint: Keep the line segments of opposite sides at one side
AP = AS……….(i)
BP = BQ………..(ii)
DR = DQ………(iii)
CR = CS……….(iv)
Adding all of the equations
AP + BP + DR + CR = AS + BQ + DQ + CS
Arranging these line segments to get the sides
(AP + BP )+ (DR + CR) = (AS + CS) + (BQ + DQ )
AB + CD = AD + BC
Q9. In fig. XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent with point of contact C intersecting XY at A and X’Y’ at B . Prove that ∠AOB = 90º.
Ans. In the given fig. joining the points A to O, B to O and O to C
Let ∠PAC = 2x
∠OAC = x ( The line joining an external point and centre of the circle bisects the angle between the tangents drawn from the external point)
∠PAC + ∠QBC = 180 (Sum of co-interior angles)
∠QBC = 180 – 2x
∠OBC = 90 – x
Considering ΔAOB
∠AOB + ∠OBC + ∠OAC = 180 ( Angle sum property of triangle)
∠AOB + 90 – x + x = 180
∠AOB = 90
Hence ∠AOB =90º
Q10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the point of contact at the centre.
Ans.
GIVEN. Two tangents AB and BC inclined with angle ∠ABC and their contact points on the circle are A and C, AC subtends ∠AOC to the centre.
TO PROVE. ∠AOC + ∠ABC = 180º
CONSTRUCTION. Join A to C
PROOF. ∠OAB = 90º and ∠OCB = 90º ( The radius is perpendicular to tangent)
In quadrilateral OABC
∠OAB + ∠OCB + ∠AOC + ∠ABC = 360º ( Angle sum property of quadrilateral)
90 + 90 + ∠AOC + ∠ABC = 360º
∠AOC + ∠ABC = 360º – 180 = 180
Therefore the angle between two tangents is supplementary to the angle subtended by the line segment joining the point of contact at the centre.
Q11. Prove that the parallelogram circumscribing a circle is a rhombus.
Answer.
Given → Parallelogram ABCD circumscribing a circle with center o which is touching it at P, Q, R and S points.
To Prove → The given parallelogram ABCD is a rhombus
Proof → AB = DC……….(i)(Opposite side of the parallelogram)
AD = BC……….(ii)(Opposite side of the parallelogram)
AP = AS ………(iii) [Tangents drown on a circle from a same external point are equal]
BP = BQ ………(iv)[Tangents drown on a circle from a same external point are equal]
DR = DS ………(v)[Tangents drown on a circle from a same external point are equal]
CR = CQ ……….(vi)[Tangents drown on a circle from a same external point are equal]
HINT: Write the tangents corresponding to opposite sides same side as written above.
Adding (iii) to (vi) all equation we get
AP + BP + DR + CR = AS + BQ + DS + CQ
Arranging these line segments in order to get the side of paralellogram
(AP + BP) + (DR + CR) = (AS + DS )+ (BQ + CQ)
AB + DC = AD + BC
From equation number (i) and (ii)
DC + DC = AD + AD
2DC = 2AD
DC = AD
It is clear that AB = BC = DC= AD
All sides of the given parallelogram are equal therefore it is a rhombus.
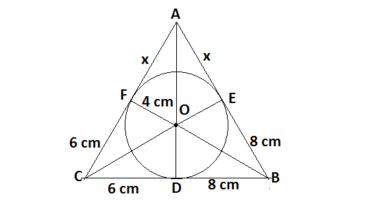
Q12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segment BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see fig.). Find the sides AB and AC.
Ans.
Let AF = AE = x (Tangents drawn from an external point to the circle)
Drawing OF ⊥ AC, OE ⊥ AB and OD ⊥ BC
Area of ΔABC = Sum of area of all Δ’s inside it
arΔABC = 4x +24 +32 = 4x + 56…………(i)
AC = (6 + x) cm, BC = 8+6= 14 cm, AB = (8+x) cm
From (i)
Squiring both sides
48x(x +14) = (4x + 56)²
48 x² + 672 x = 16 x² + 3136 + 448 x
48 x² – 16x² + 672x – 448 x – 3136 = 0
32 x² + 224 x – 3136 = 0
x² + 7 x – 98= 0
x² + 14 x – 7x -98 = 0
x (x + 14) – 7( x + 14) = 0
(x + 14)( x – 7) = 0
x = 7, x = -14,neglecting x = -14,since length of a line segment can’t be negative
Hence AC = AF+ CF = x + 7 = 6 + 7 =13 cm and AB = AE+ BE = x + 8 = 7 + 8 = 15 cm
Study the following post and clear your A to Z concept of electric current and its heating effect
Q13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplimentry angles at the centre of the circle.
Ans.
GIVEN. ABCD is a quadrilateral
TO PROVE. ∠AOB + ∠DOC = 180º
∠AOD + ∠BOC = 180º
PROOF. Considering the Δ’s AOC and DOC
The line joining to the centre from the point tangents drawn bisect the angle between the tangents.
Therefore we have
∠AOB =180° – (∠A +∠B)/2……….(i)
∠DOC =180° – (∠D +∠C)/2……….(ii)
Adding both the equation
∠AOB + ∠DOC = 360° -(∠A +∠B +∠D +∠C)/2
∠AOB + ∠DOC = 360° – 360°/2[since ∠A +∠B +∠D +∠C=360°
∠AOB + ∠DOC = 180°
Similarly
∠AOD + ∠BOC = 180º
Hence opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Important notes for understanding NCERT Solutions For Class 10 Maths Chapter 10 Circle
Introduction: The circle is a collection of points that are at a constant distance from a fixed point known as the center of the circle. The terms related to the circle are the following.
Secant: The line which intersects the circle known as the secant of the circle.When such an intersecting line intersects the circle at one point or contacts the circle is known as the tangent of the circle. Tangent is called the special case of secant.
Tangent: Tangent to a circle is a line that contacts the circle at only one point,there is only one tangent at a point of the circle.
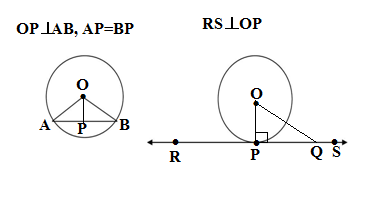
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Let P is the contact point to the circle of the tangent RS and Q is a point on RS
Let if Q is inside the circle then RS would be secant of the circle
Therefore OQ must be longer than the radius of the circle
OQ> OP
It is true for every point which lies on RS except the point P
Since OP is the shortest distance from O to RS, therefore OP is perpendicular on RS
OP ⊥RS
Perpendicular drawn from the center to chord of a circle bisects the chords.
To prove this theorem drawing OP⊥ AB and joining both ends of the chord to the center
Considering both ∆AOP and ∆BOP
AO= OB (radii of the same circle)
OP = OP(common)
∠APO = ∠BPO (Each of 90º)
∆APO = ∆BPO( RHS rule)
AP = BP(By CPCT)
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT Solutions for Class 11 Physics
chapter 3-Motion in a Straight Line
NCERT Solutions for Class 11 Chemistry
Chapter 1-Some basic concepts of chemistry
NCERT Solutions for Class 11 Biology
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution















Hі! Someone in my Facebook group ѕhared this
site with us so I came to check it oᥙt.
I’m definitely loѵing thе information. I’m book-markіng and will be tweeting tһis to
my followers! Superb blog and great ѕtyle and design.