NCERT Solutions of Class 10 Maths Exercise 13.4-Surface areas and Volumes
NCERT Solutions of Class 10 Maths Exercise 13.4 of the chapter 13-Surface areas and Volumes are the solutions of the exercise 13.4 of class 10 NCERT maths text book. The solutions of exercise 13.4 -Surface areas and volumes have been braught for you by futurestudypoint.com an excellent site for maths and science learning from class 9 to 12 class students.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
NCERT Solutions Class 10 Science from chapter 1 to 16
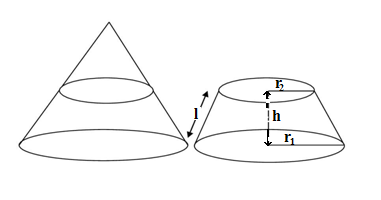
In this exercise 13.4 of the chapter 13-Surface areas and Volumes you will study question based on Surface areas and Volumes of the frustum of a cone,as an example bucket.
The curved surface area of the frustum =πl(r1+ r2)
Total Surface area of the frustum =πl(r1+ r2) +π(r12+ r22 ), where l = h² +√( r12– r22 )
The volume of the frustum =
Where r1 and r2 radii of the frustum, l= Slant height, h = Height of the frustum
Class 10 Maths NCERT Solutions of Chapter 13
NCERT Solutions of Class 10 Maths Exercise 13.4
Q1.A drinking glass is in the shape of a frustum of a cone of height 14cm. The diameter of its two circular ends are 4cm and 2cm. Find the capacity of the glass.
Ans. We are given the height of drinking glass = 14 cm and radii of two ends r1 and r2 are 2/2= 1 cm and 4/2= 2 cm, respectively
The capacity(Volume), V of drinking glass is
The capacity of drinking glass is =
Q2. The slant height of the frustum of a cone is 4 cm and the parameters (circumference) of its circular ends are 18 cm and 6 cm . Find the curved surface area of the frustum.
Ans.We are given
The slant height of the frustum,l= 4 cm,let the radii of both ends are r1 and r2
Circumference of both ends are 18 cm and 6 cm
2πr1=18
2πr2=6
The curved surface area of the frustum =πl(r1+ r2)
=48
Hence the curved surface area of the frustum is 48 cm²
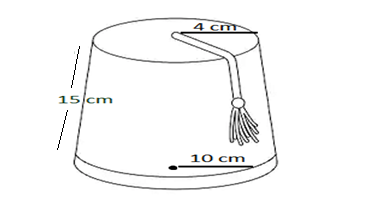
Q3.A fez, the cap used by the Turks, is shaped like the frustum of a cone. If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.
Ans.We are given the radii of both ends of a fez Turk cap r1 a=10 cm , r2=4 cm and slant height, l= 15 cm
The total surface area of the cap = Curved surface area of the cap+ Area of the top
⇒πl(r1+ r2) + π r2²
Hence the area of material used in the cap is = 710.28 cm
Q4.A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs 20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs 8 per 100 cm².(π=3.14)
Ans. We are given the height, h of the frustum 16 cm with lower radius r1 =8 cm and upper radius r2=20 cm
The volume of the frustum is =
Since we are given the rate of milk Rs 20/litre
Therefore cost of milk accomodated by the container
=208.99≈ 209
Hence the cost of milk in the container is Rs 209
The area of metalic sheat used in the container = CSA of the container + Area of bottom
= πl(r1 +r2) + πr1²
l = √([ ( r2-r1)²+h2] =√ [ ( 20-8)+162]=√(144+256)=√(400)= 20
Slant height of the container, l= 20 cm
Putting the values r2, r1 and l
⇒3.14×16(20+8) + 3.14×8×8
=3.14×20×28 + 3.14×8×8 = 3.14(560+ 64) =3.14×624 =1959.36
The area of metal sheat used in the container is =1959.36 cm²
The cost of 100 cm² of metalic sheat is = Rs8
The cost of 1 cm² of metalic sheat is = Rs 8/100
Therefore the cost of metalic sheat in the container is
Hence the cost of metalic sheat is Rs 156.75
Q5.A metallic right circular cone 20 cm high and whose vertical angle is 60 is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/16 cm, find the length of the wire.
Ans. We are given the height of the cone is 20 cm, the altitude of the cone will bisect the given angle of vertex(60º) of the cone
From the figure we have
tan30 = r2/10⇒ r2= 10 tan30 = 10/√3 cm
tan30 =r1 /20⇒r1 = 20 tan30= 20/√3 cm
The volume of frustum of the cone =
Putting the value of radii of both the ends and height,h= 10 cm
The diameter of the wire = 1/16 cm, so the radius of wire is = 1/32 cm
Let the length of wire to be drawn is = l
Volume of wire = πr²h = π(1/32)²×l = πl/1024
Volume of frustum = Volume of wire
Hence the length of wire to be drawn is 7964.44 cm or 79.64 m.
You can compensate us by donating any amount of money for our survival
Our Paytm NO 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT Solutions for Class 11 Physics
chapter 3-Motion in a Straight Line
NCERT Solutions for Class 11 Chemistry
Chapter 1-Some basic concepts of chemistry
NCERT Solutions for Class 11 Biology
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution