Class 9 Science NCERT solutions of  chapter 8-Motion

The NCERT solutions of class 9 science NCERT textbook chapter 8 – Motion are helpful to understand the concept of scientific facts of chapter 8-Motion.The NCERT solutions of class 9 science NCERT textbook chapter 8 – Motion are helpful to understand the concept of kinematics which is one of the branches of physics. The NCERT solutions of chapter 8-Motions of science NCERT textbook will clear all your doubts and concept of the chapter 8-motion. The NCERT solutions of chapter 8-motion are designed here for your help in boosting the preparation of CBSE Board exams and in your homework assigned by the school. All NCERT solutions are solved by an expert science teacher as per the CBSE norms.

Why are the NCERT solutions of class 9 science NCERT textbook chapter 8 – Motion are important?

• Clears the basic scientific idea of ‘ Motion’ that is needed in a higher class.
• Helpful in studying other chapters of physics.
• These are Important for the CBSE Board exam.
• Students can exploit these in getting a better score in the exam.
• Covers solution of all questions page-wise and back exercise

 

You can study here class 9 science NCERT solutions of all chapters, the links are given for each chapter.

Related notes on chapter 8-Motion.

What is the difference between Distance and Displacement

What is the difference between Speed and Velocity?

Average Speed and Average Velocity: Differences

 

Science NCERT Solutions of Chapter-8

You can download PDF-NCERT solutions of Class 9 science chapter 8 -Motion

PDF-Class 9 Science NCERT Solutions of Chapter-8 Motion

Q1 – An object has moved through a distance. Can it have zero displacements? If yes, support your answer with an example.

Ans – Yes. An object moved through a certain distance and returned back to the same position then its displacement would be zero. Let an object moves x km in a direction and then moves x km in a negative direction then the displacement covered by the object = x – x = 0.

Q2- A farmer moves along the boundary of a square field of side 10 m in 40 s What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?

Ans. For the measurement of the displacement, we have to calculate how much rounds the farmer has completed of the square field. Let the farmer starts to move from point A of the following square field.

Distance covered in one round =Perimeter of the square field = 4 ×10 = 40 m Time taken by him = 2 min 20 seconds = 2×60 + 20 =140 seconds

In 40 seconds farmer makes = 1 round

In 140 seconds he will make = (1/40) × 140 =7/2 = 3 and ½ round

After 3 and 1/2 round his position will be at C

So-net displacement from his initial position A is = AC = (√(10² + 10²) = √200 = 10√2 m Ans.

Q3. Which of the following is true for displacement?

(a) It can not be zero.

(b) Its magnitude is greater than the distance traveled by the object.

Ans. (a) is false, let A travels a distance of 100 m towards in the direction of the east and return back to the same point then displacement of A will become 0.

(b) is false, let A travels 100 m in the direction of the east and then 50 m in the direction of the west then displacement of A will be 100 – 50 = 50 m,

while the distance covered by him = 100 + 50 = 150 m.

Q4. Distinguish between speed and velocity?

Ans .

Speed – The distance covered in one unit time is known as speed, speed is a scalar quantity because for its representation the only magnitude is required.

Velocity- The displacement covered in one unit time is known as velocity, velocity is a vector quantity because for its representation magnitude as well as direction is needed in short speed with direction is known as velocity.

Q5. Under what condition is the magnitude of the average velocity of an object equal to its average speed?

Ans. The average velocity of an object is equal to its average speed when total displacement covered by an object is equal to the total distance covered by it.

Q6, What does the odometer of an automobile measure?

Ans. The odometer of an automobile is used for measuring the distance.

Q7. What does the path of an object look like when it is in uniform motion?

Ans. The path of an object is a straight line in uniform motion.

Q8.During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is 3×10⁸ m /s

Ans. Time = 5 minutes = 5 ×60 = 300 seconds

Speed of light = 3 ×10⁸ m/s

Distance covered by the signal = speed x time = 300 × 3× 10⁸= 9 ×10¹⁰ meter

So distance of the spaceship from the ground station = 9 × 10¹⁰ meter

Q9. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?

Ans. Distance -time graph for uniform motion shows a straight line while for non-uniform motion it shows a curved or zig-zag line.

 

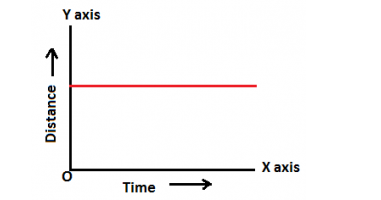
Q10. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?

Ans. The distance-time graph parallel to the time axis shows that the object is not moving, it is in the rest position.

 

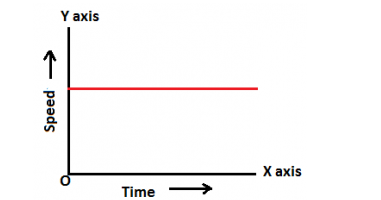
Q11. What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time axis?

Ans. Speed-time graph parallel to the time axis shows the object is moving with a uniform speed and its acceleration is zero.

 

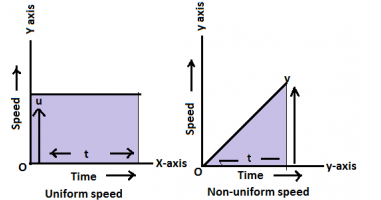
Q12. What is the quantity which is measured by the area occupied before the velocity-time graph?

Ans. Distance = Velocity x time, in case of uniform velocity the velocity-time graph shows a shape of the rectangle if the object moves with the velocity u within the time interval of t. So in the same way when the object moves with accelerated speed the area covered by the speed-time graph shows the distance covered by the object in time t.

 

If speed is substituted in the given question then the area of velocity-time graph will show the total displacement

Q13. A bus starting from rest moves with a uniform acceleration of 0.1 m/s² for 2 minutes. Find

(a) the speed acquired. (b) the distance traveled.

Ans. Since the bus starts from the rest so its initial velocity, u = 0

(a)  Acceleration, a = 0.1 m/s², Time,t = 2 minutes = 2 ×60 = 120 s

v = u + at

v = 0 + 0.1 × 120 = 12

So the bus will acquire a speed of 12 m/s.

(b) Applying second equation of the motion

S = ut +(1/2 )at²

u=0,a =0.1 m/s², t=120 s

S = (1/2) ×0.1×(120)² = (14400×0.1)/2 = 720 m

The distance traveled by the train = 720 m

 

Q14. A train is traveling at a speed of 90 km/h. Brakes are applied so as to produce a uniform acceleration of -0.5m/s2. Find how far the train will go before it is brought to rest.

Ans. Initial speed u = 90 km/h = (90 ×1000)/60×60 = 25 m/s

Acceleration, a= −0. 5 m/s²

Final velocity,v = 0 since the train is brought to rest. Distance traveled by train, s =?

Applying the third equation of the motion

v² = u² + 2as

0 = 25² + 2 × −0.5×s

s = 625

So the train will go 625 m before it is brought to rest.

See the video for question number 1,2 and 14

Q15. A trolley, while going down an inclined plane, has an acceleration of 2 cm/s². What will be its velocity 3 s after the start?

Ans. Intial velocity of the the trolley,u = 0 since before it is going down it was in rest position,Acceleration, a = 2 cm/s² = 0.02 m/s² , time, t= 3 s

V = u + at

V = 0 + 0.02 × 3 =0.06

So the speed of the trolley after 3 s will be 0.06 m/s

Q16. A racing car has a uniform acceleration of 4 m/s². What distance will it cover in 10 s after start?

Ans. Since the car starts from the rest position so, u = 0, Time,t = 10 s, Acceleration, a = 4 m/s2

Applying the second equation of the motion.

So after 10 s, the car will cover a distance of 200 meters.

Q17. A stone is thrown in a vertically upward direction with a velocity of 5 m/s . If the acceleration of the stone during its motion is 10 m/s2 in the downward direction, what will be the height attained by the stone and how much time will it to reach there?

Ans. The initial velocity of the stone, u = 5 m/s, The stone is under the impact of gravitational force, so acceleration exerted on the stone,g = −10 m/s2  (Its sign is negative because the direction of gravitational force is opposite to the direction of motion), Height obtained by the stone,h =? , v = 0 since after the height  achieved by the stone it will rest before returning to the earth, The time is taken in achieving the height, h is = t

Applying the third equation of the motion.

v² = u² + 2gh

0 = 5² + 2 × – 10 × h

20h = 25

h = 25/20 = 1.25

h= 1.25 m

The height obtained by the stone is = 1.25m

For getting the time(t) to reach that height applying the first equation of the motion.

V = u + gt

0 = 5 +( −10) × t

10 t = 5

t = 0.5

So the time taken to achieve that height will be 0.5 seconds and the stone will reach the height of 1.25 meters.

See the video for solutions of question 13,15,16 and 17

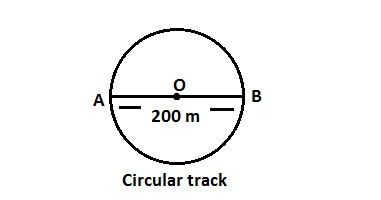
Q18.An athlete completes one round of a circular track of diameter 200 m in 40 s . What will be the distance covered and the displacement at the end of 2 minutes 20 s?

Ans. In the calculation of the displacement at this situation, we have to determine how many rounds the athlete will take in a given time.

Given time , 2 minutes 20 minutes = 2 ×60 + 20 = 140 seconds

In 40 seconds athlete takes = 1 round

In 140 seconds he will make = (1/40)×140 = 3 and 1/2 round

 

If the athlete starts from a point A, then after 3  and 1/2 round his position will be at another end B of the diameter So the displacement of the athlete will be AB = 200 meter

 

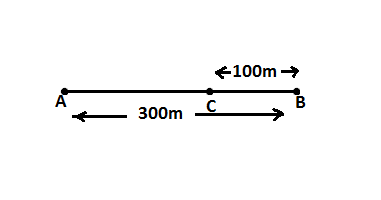
Q19. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging (a) from A to B and (b) from A to C?

Ans.

( a) Total distance covered by Joseph from A to B = 300 m

Total time is taken to cover the distance from A to B = 2 min 30 s= 2 × 60 + 30 =150 s

The average speed = 2 m/s.

Displacement covered from A to B = 300 m

Time taken from A to B = 2 minute 30 seconds  = 150 seconds

The average velocity = 2 m/s

Hence the average speed  is 2 m/s and the average velocity is 2 m/s of Joseph in traveling from A to B

(b) Total distance covered from A to C = 300 + 100 = 400 meter

Total time  is taken from A to C = 1 minute + 150 seconds = 210 seconds

Total displacement from A to C = 300 – 100 = 200 m

Total time  is taken from A to C = 210 seconds

Hence the average speed is 1.90 m/s and the average velocity is 0.95 m/s of Joseph in traveling from A to C.

Q20. Abdul, while driving to school, computes the average speed for his trip to be 20 km/h.On his return trip along the route, there is less traffic and the average speed is 30 km/h. What is the average speed for Abdul’s trip?

Ans. Let the distance of his school from his home is = x km

The average speed of Abdul from home to school is = 20 km/h

So the time is taken to reach the school = distance/ speed =(x/20) h

The distance from school to home = x km

The average speed of Abdul from school to home = 30 km/h

So, the time is taken from school to home =( x/30)h

Total distance covered by Abdul from home to school and school to home = x + x= 2x

Total time taken by Abdul in the trip = (x/20)  + ( x/30)= (x/12) h

So Abdul’s average speed  in the whole of the trip is = 24 km/h

Q21.A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m/s² for 8.0 s.How far does the boat travel during this time?

Ans. Since motorboat starts from rest position so, the initial speed of motorboat, u = 0, Acceleration, a = 3 m/s², Time, t = 8 s, Distance traveled by the motorboat in the given time, s =?

Applying the second equation of the motion.

So the boat will travel a distance of 96 meters.

See the video for the solutions of Q20 and Q21 and please subscribe to the channel for the next videos.

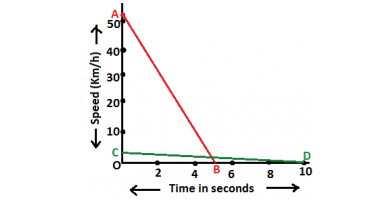
Q22. A driver of a car traveling at 52 km/h applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 km/h in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars traveled farther after the brakes were applied?

Ans. Speed –time graph of both cars is the following.

 

 

The distance covered by the car 1 = area of the triangle made by the graph

The distance traveled by car which is traveling with the speed 52 km/h = Area of ΔAOB

The distance traveled by car which is traveling with the speed 3 km/h = Area of ΔCOD

Area of ΔAOB > Area of ΔCOD

Therefore the distance covered by the car which is moving with 52 km/h is more.

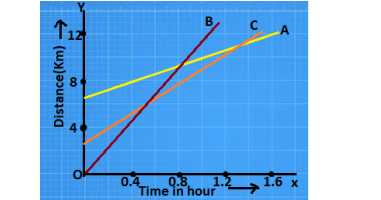
Q23. Fig 8.11 shows the distance time-graph of three objects A, B, and C.study the graph and answer the following questions:

 

 (a) Which of the three is traveling the fastest?

(b)Are all three ever at the same point on the road?

(c) How far has C traveled when B passes A?

(d)How far has B traveled by the time it passes C?

Ans. (a) The slope of B is more compared with A and C, so B is traveling faster than A and C.

(b) Since all of the graphs don’t intersect one another so the objects never meat at the same point.

(c)Object B passes A in 0.8 s, so according to this graph the distance traveled by C in 0.8 s = final position – Initial position

The final position of C at 0.8s = 8 km

The initial position of C = 6 units of graph

4 km = 10 units

1 unit = 0.4 km

The initial position of C =  6 × 0.4 = 2.4 km

Therefore distance traveled by C = 8 –2.4 =5 6 km

 

(d) B passes C at 0.6 s, so at  0.6 the distance traveled by B = Final position of B – Initial position of B

The final position of B at 0.6 s is = 6 km and the initial position of B is  = 0 km

Therefore B traveled by the time it passes C = 6 km

Q24. A ball is gently dropped from a height of 20 m, its velocity increases uniformly at the rate of 10 m/s², with what velocity will it strike the ground? After what time will it strike the ground?

Ans. The height of the ball therefrom it is dropped, h = 20 m

The acceleration, a = 10 m/s²

The velocity the ball strikes the ground,v=?

Since the ball starts from its rest position, so initial velocity, u= 0

The time on which the ball strikes the ground,t=?

Applying the third equation of motion

v² = u² + 2gh

v² = 0² + 2 × 10 × 20

v = 20

The ball strikes to the ground with 20 m/s velocity

Applying the first equation of motion

v = u + gt

20 = 0 + 10 × t

t = 2

Hence the ball strikes the ground after 2 second with 20 m/s velocity.

 

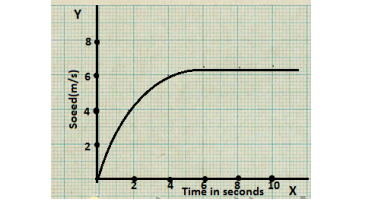
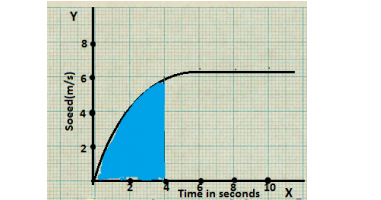
Q25. The speed-time graph for a car is shown in fig.8.12.

 

(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance traveled by car during the period (b) Which part of the graph represents the uniform motion of the car?

Ans. In the speed-time graph, the area formed by the graph in a given time is equal to the distance covered, the area formed in 4 seconds is shown bellow in shaded shows the distance covered.

 

The area of shaded region = 1/2(4 ×6) = 12 square meter

So, the distance covered in 4 seconds = 12 meter

(b) The speed of the car remains the same after the 6 seconds, so from 6 seconds onwards, the graph represents uniform motion.

 

Q26. State which of the following situation are possible and give an example for each of these (a) An object with a constant acceleration but with zero velocity (b) An object moving with acceleration but with uniform speed (c) An object moving in a certain direction with an acceleration in the perpendicular direction.

Ans.

(a) The situation of an object with a constant acceleration but with zero velocity can exist in the case when the objects move against the constant force of gravity as an example a stone is thrown in upwards direction moves with a constant acceleration of 9.8 m/s² and at the maximum height, its speed becomes zero.

(b) The situation of an object moving with acceleration but with uniform speed is impossible because uniform speed means there is no change in speed.

(c) The situation of an object moving in a certain direction with an acceleration in the perpendicular direction is possible in case of circulatory motion. As an example moon is revolving around the earth but the direction of acceleration is in a perpendicular direction to the tangents to the circular path on which moon is moving.

Q27.An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.

Ans. The radius of the circular path of the satellite is =42250 km

The distance covered by satellite in one revolution = 2πr = 2 × 22/7 ×  42250 =265571.43 Km

Time is taken to cover the distance of one revolution = 24 h

Speed of satellite = distance/time = 265571.43/24 =11065.48 km/h

Class 9 CBSE Science Notes

Three Laws of Motion: Class 9 CBSE

Evoporation,Vapourization and Latent heat -Class 9 CBSE notes

What is an atom,molecule and atomicity of a substance?

How to determine Valency,net charge of an ion and Molecular formula of a substance.

Thrust and Pressure : Difference

The Complete Detail of Archimedes Principal

Average Speed and Average Velocity: Differences

How to evaluate recoil velocity of gun

If energy is conserved then why do we need to save it for future generations?

Molar mass,molecular mass and mole concept

What is second law of of motion ?

What is universal law of gravitational force

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of Class 10 Science Sample Paper and Question Papers for Term-1 and Term 2 2021-22 CBSE Board

Solution of Class 10 Science Question Paper Preboard 2021-22:Term 2 CBSE Board Exam

Solutions of Class 10 Science Sample Paper Term-1 2021-22 CBSE Board

Class 10 Science Sample Paper for Term 2 CBSE Board Exam 2021-22 with Solution

Solutions of Class 10 Science Question Paper Preboard Examination (First) 2021 -22 Class 10 Science

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Sample paper of Science 2020

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE