Spring Force:Class 11 CBSE Physics Chapter 5

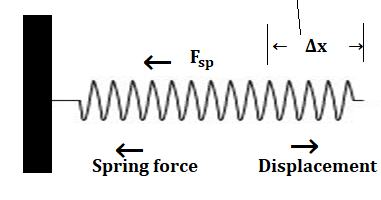
The spring force is not so different from the force of string(Tension),here both of the mass of string and spring are supposed as massless,the spring force(F) is directly proportional to the displacement(Δx) in the direction of force.The spring force is the same if it is stretched or compressed by the same magnitude but its direction is always opposite to the direction displacement.

 

Let a spring is stretched by a force F_SP  to a displacement of Δx

The spring force is directly proportional to the displacement Δx

F_SP  ∝ Δx

The minus sign shows that the direction of spring force is opposite of the displacement or elongation

∴F_SP  = -kΔx

Where k is the constant force of the spring and depends on the type of spring,the spring force is a variable force,it increases with the increase of elongation Δx.

If the spring is compressed then the spring force will be in opposite direction.The spring force, F_SP is same at every point of the spring in case of the same spring.

If a spring is pulled by two persons,the displacement of the spring in both sides are x₁ and x₂

Then net elongation is

Δx = x₁ + x₂

The spring force will be the same at every point of the spring and its value is

F_SP = -k(x₁ + x₂)

In case of spring and string the spring force and the force of tension have the same value at every corresponding points of them when both are considered mass less.

Example: Two blocks A and B are attached to the same spring ,k=50N/m. Then find

(a)The spring force when blocks A and B are displaced by 1 m on both sides.

(b)The spring force when blocks A and B are displaced by 1 m in the same direction.

Solution. For both cases (a) and (b) the images are shown below.

(a)The displacement,of the block is 1m

Spring force is

F_SP = -kΔx

Neglecting the minus sign since we are needed to evaluate only the magnitude of spring force

F_SP = kΔx

Displacement ,Δx = 1 +1 = 2m

F_SP = 50×2 = 100N

 

(b) The net displacement ,Δx = 1-1 =0

F_SP = 50×0 = 0N

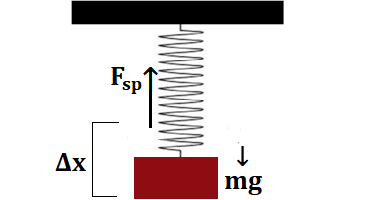
The calculation of the elongation when a weight is suspended on a spring :

Let a solid of the mass m is suspended on a spring and spring is displaced by Δx then the spring force is

F_SP = kΔx

Since spring is supposed as it is in equilibrium condition

F_SP = mg

mg = kΔx

Δx = mg/k

If mass m and value of k is given then we can calculate the displacement of the spring.

Static and Kinetic Friction :Class 11 CBSE Physics Chapter 5

Forces and Newton’s First Laws of motion:Class 11 Physics Chapter 5 CBSE

Newton’s Third Law of the Motion and Conservation of the Momentum:Class 11CBSE Physics

You can also study class 11 Physics and Chemistry Notes

Circular Motion: Angular velocity and angular displacement

Projectile Motion Class 11 CBSE Physics Chapter 4 Motion in a Plane

Addition of Vectors: CBSE Class 11 Physics Chapter 4 -Motion in a Plane

Don’t forget to write a comment, subscribe us for the posts related to your study

Lattice Energy Class 11 CBSE Chemistry Chapter 4

Electronic Configuration of s,p and d orbitals

Atomic Radius Class 11 Chemistry Chapter 3 Periodicity in Properties

Why does a Rainbow look like a Bow?

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT Solutions for Class 11 Physics

Chapter 1- Physical World

chapter 3-Motion in a Straight Line

NCERT Solutions for Class 11 Chemistry

Chapter 1-Some basic concepts of chemistry

Chapter 2- Structure of Atom

NCERT Solutions for Class 11 Biology

Chapter 1 -Living World

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution