The projectile motion of an object thrown from a certain height : Class 11 Physics
The projectile motion of an object thrown from a certain height:If an object is thrown from a certain height by an angle θ with a velocity of u, the velocity u will have two components, horizontal ux and vertical uy , here ux remains the same because the acceleration along the x-axis is zero while the vertical component uy of velocity first decreases upto a certain height and then increases downwards achieves its maximum value nearest to the ground, the gravitational acceleration will always be negative because it has been applied on the vertical component of the velocity.
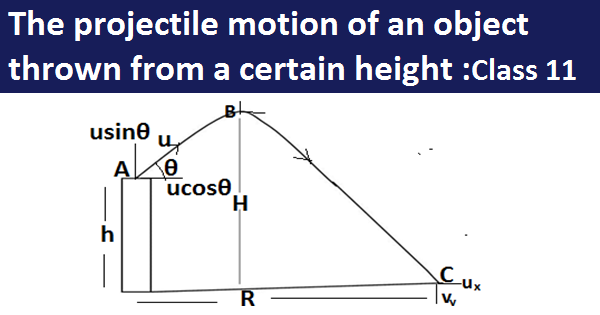
The projectile motion of an object thrown from a certain height :
The projectile motion of an object thrown from a certain height:Let an object is thrown from the top of a tower of the height h, the velocity of the object,u will have two component horizontal ux and vertical uy the path of the object is of parabolic shape because the object is dragged vertically and horizontally by both component of velocity, the vertical component will become 0 when it achieves a maximum height of H.
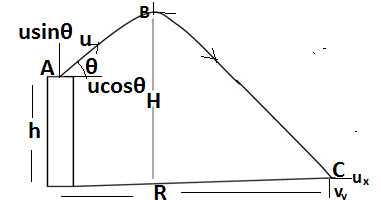
The displacement covered by the object in reaching from A to C is = -h
The time taken by the object in the journey is = T
Since displacement is along the y-axis.so let us take y component of velocity
Acceleration = -g(since it acts on the vertical component of velocity)
The initial velocity of the object = usinθ
Applying the second equation of the motion
s = ut +( 1/2)at²
-h =usinθ.T + ( 1/2)(-g)T²
( 1/2)(g)T²- usinθ.T -h =0
gT²- 2usinθ.T -2h =0…….(i)
Solving this quadratic equation, we can get the time taken by the object from the top of the building to the ground.
The range of the object is actually the displacement of the object in the direction of the x-axis
The time taken from the equation (i) is = T
The initial velocity of the object in the direction of the x-axis is = ucosθ
Acceleration along the x-axis is =0
The displacement along the x-axis = R
Applying the second equation of the motion
s = ut +( 1/2)at²
R = ucosθ.T + ( 1/2)×0×t²
R = uTcosθ……(ii)
Therefore we can calculate the range and time is taken by the object to reach the ground when it is thrown by an angle θ from a certain height from the ground
The projectile motion of an object thrown from a certain height
The final velocity of the object just before hitting the ground: The x component of the velocity remains the same even when it reaches to the ground at point C , the velocity which is changing is the vertical component, which was initially usinθ finally would become vsinθ
The acceleration along y-axis = -g
Applying the first equation of motion
v = u + at
vcosθ = ucosθ – gT
v = (ucosθ -gT)/cosθ
Finding the height of the tower when an object is thrown with a particular velocity of u downwards by an angle of θ from the horizon:
The height of the tower is =displacement in the direction of y axis =h
The initial velocity of the object is =-usinθ(- sign shows because the object is thrown in a downward direction)
The acceleration is = -g(since the displacement and gravitational acceleration are opposite to each other)
Displacement in the direction of x-axis is =R
Acceleration in the direction of x-axis is = 0
The initial velocity in the x direction is =ucosθ
Applying the second equation of the motion
s = ut +( 1/2)at²
R= ucosθ.T(since a =0)
T = R/ucosθ.
Applying the second equation of the motion
s = ut +( 1/2)at²
h = usinθ.t -( 1/2)gT²
Projectile Motion:A particle moves along a curved path under constant acceleration when thrown obliquely near the surface of the earth. This curved path is always directed towards the centre of the Earth. The path of such a particle is called the trajectory of the projectile, and the motion is called the projectile motion
We hope you would have liked the post ‘The projectile motion of an object thrown from a certain height ‘this topic is taken from the class 11 NCERT physics textbook which is very important to understand for solving the numerical of physics in class 11 CBSE Board exams.
Circular Motion: Angular velocity and angular displacement
Projectile Motion Class 11 CBSE Physics Chapter 4 Motion in a Plane
Addition of Vectors: CBSE Class 11 Physics Chapter 4 -Motion in a Plane
Don’t forget to write a comment, subscribe us for the posts related to your study
Electronic Configuration of s,p and d orbitals
Atomic Radius Class 11 Chemistry Chapter 3 Periodicity in Properties
Why does a Rainbow look like a Bow?
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT Solutions for Class 11 Physics
chapter 3-Motion in a Straight Line
NCERT Solutions for Class 11 Chemistry
Chapter 1-Some basic concepts of chemistry
NCERT Solutions for Class 11 Biology
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution



