Class 11 Maths solutions of important questions of ‘Sets’

Class 11 Maths solutions of important questions of chapter 1-Sets are going to help every maths student of class 11 in boosting their preparation for the class 11 exam of CBSE board. The solutions of important questions of chapter 1-Sets will clear your basics of maths which is required to study for gaining higher maths study. All questions are solved by an expert teacher of maths as per the CBSE norms. All important questions of chapter 1- sets of class 11 CBSE are solved in a step by step method.

Class 11 Maths solutions of important questions of chapter 1-Sets

Study the basics of the Sets, see the video

Q1.If A = { 1,2,3,4,5,6}, B = {2,4,6, 8} then find A – B.

Ans.We are given the sets A ={ 1,2,3,4,5,6}, B = {2,4,6, 8}

A – B = { 1,2,3,4,5,6}- {2,4,6, 8} = {1, 3, 5}

Q2. Let A and B be two sets containing 3 and 6 elements respectively. Find the maximum and the minimum number of elements in A ∪ B.

Ans.There may be the case when atleast 3 elements are common between both sets

Let a set A = {a, b, c} and B = {a, b, c, d, e, f}

∴ A ∪ B = {a, b, c, d, e, f} implies that the minimum number of elements in A ∪ B are = 6

There may be the case when there are no any elements are common between both sets

lf A = {a, b, c}, B = { d, e, f, g, h, i}

A ∪ B = {a, b, c, d, e, f,g,h,i} implies that the maximum number of elements in A ∪ B are = 9

Q3.If A = {(x,y) : x² + y²= 25 where x, y ∈ W } write a set of all possible ordered pair .

Ans. We are given the set A = {(x,y) : x² + y²= 25 where x, y ∈ W }

All possible ordered pair of set A are following

For x = 0,y =5, x=3,y=4,for x =4, y =3,for x=5,y =0

A = {(0,5),(3,4),(4,3),(5,0)}

Q4.If A = {1,2,3}, B = {4, 5, 6} and C ={5} verify that A ∪ ( B ∩ C) = (A ∪ B) ∩ A ∪ C.

We are given the sets A = {1,2,3}, B = {4, 5, 6} ,C = {5}

B ∩ C = {5}

LHS

A ∪ ( B ∩ C) = {1,2,3,5}

(A ∪ B) and A ∪ C

A ∪ B = {1,2,3,4,5,6} and A ∪ C = {1,2,3,5}

RHS

(A ∪ B) ∩ A ∪ C = {1,2,3,5}

Therefore

A ∪ ( B ∩ C) = (A ∪ B) ∩ A ∪ C, Hence proved

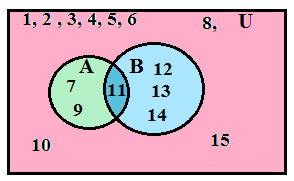
Q5.From the adjoining Venn diagram, write the value of the following.

(a) A ‘

(b) B’

(c) (A ∩ B)’

Ans. From the venn diagram ,we have

U = {1,2,3,4………15}

A = {7,9.11}. B ={11,12,13,14}

A’ = U – A = {1,2,3,4………15} – {7,9.11} = {1,2,3,4,5,6,8,10,12,13,14,15}

B’ = U – B = {1,2,3,4………15} – {11,12,13,14}= {1,2,3,4,5,6,7,8,9,10,,15}

We have,(A ∩ B) = 11

(A ∩ B)’ = U – (A ∩ B) = {1,2,3,4………15} – {11} = (1,2,3,4,5,6,7,8,9,10,12,13,14,15}

Q6. If P(A) = P(B) show that A = B.

Ans. P(A} and P(B) implies that both are power sets of A and B respectively

Every set is an element of its power set , so A ∈ P(A)

Since, we are given that

P(A) = P(B)

Therefore, A ∈ P(B)

Indicates that every element of A belongs to the set B

So, A ⊂ B……(i)

Similarly B ∈ P(B)

Since, we are given that

P(A) = P(B)

Indicates that every element of B belongs to the set A

So, B ⊂ A……(ii)

From (i) and (ii), we get

A = B, Hence proved

Click-For online purchasing of Computer and Accessories

Q7. Let A and B be sets ; if A∩X = B∩X = ∅ and A∪X = B∪X for some set X.Show that A=B.

Ans. We are given that A∩X = B∩X = ∅ and A∪X = B∪X

To prove A=B

Proof. A∪X = B∪X (given)

Multiplying both sides by A∩

A∩ (A∪X) =A∩ (B∪X)

Using distributive property

(A∩ A) ∪ (A ∩ X) = (A∩ B )∪ (A∩ X)

A∩Φ = (A∩ B) ∪ Φ

A = (A∩ B) …………(i)

A∪X = B∪X

Multiplying both sides by B∩

B∩(A∪X) = B∩(B∪X)

(B∩ A) ∪ (B ∩ X) = (B∩ B )∪ (B∩ X)

(B∩ A) ∪φ = B ∪ φ

B = (B∩ A)

B = (A∩ B) …………(ii)

From (i) and (ii)

A = B, Hence proved

Q8.If A ={1,2,3,4,5},then write the proper subsets of A.

Ans. The number of elements in the given sets A ={1,2,3,4,5} are =5

The number of proper subsets of any set are = 2ⁿ – 1

^{Where n = number of elements = 5}

^{The number of proper subsets of any set are =}2⁵ – 1 =32 – 1 = 31

Q9.Write the following sets in the Roster form

(i) A={x : x ∈ R, 2x+11 =15}

(ii)B={x |x² =x, x ∈ R}

(iii)C={x = x is a positive factor of the prime number p}

Ans.(i)We have, A={x : x ∈ R, 2x+11 =15}

2x+1= 15 ⇒x= 2

∴ A = {2}

(ii)We have,B={x |x² =x, x ∈ R}

∴ x² = x ⇒ x²-x= 0 ⇒x(x-1)= 0 ⇒x=0,1

∴ B ={0,1}

(iii)We have, C={x = x is a positive factor of the prime number p}

Sice positive factors of a prime u∪mer are 1 ad the number itself,we have

C={1,p}

Q10.For all sets A,B and C show that (A – B) ∩(A – C) = A – (B ∪ C).

Ans. Considering that

x ∈ (A – B)∩(A – C)

⇒ x ∈ (A – B) and x ∈ (A – C)

⇒ (x ∈ A and x∉ B) and (x ∈ A and x∉ C)

⇒ (x ∈ A ) and (x ∉B and x∉ C )

⇒(x ∈ A ) x∉ (B ∪C)∈

⇒x ∈ A – (B ∪C)

⇒(A – B) ∩(A – C)⊂A – (B ∪ C)…….(i)

Now,Considering that

y ∈A – (B ∪ C)

⇒ y ∈A and y ∉ (B ∪ C)

⇒y ∈A and (y ∉B and y ∉ C)

⇒(y ∈A and y ∉B) and (y ∈A and y ∉ C)

⇒y ∈ (A – B) and y ∈ (A – C)

⇒y ∈ (A – B) ∩ y ∈ (A – C)

⇒A – (B ∪ C) ⊂(A – B) ∩(A – C)………(ii)

From (i) and (ii)

(A – B) ∩(A – C)= A – (B ∪ C), Hence proved

Q11.Let A,B and C be the sets such that A∪B = A∪C and A ∩B = A ∩C,show that B = C.

Ans. According to question, A ∪ B = A ∪ C and A ∩ B = A ∩ C

To show, B = C

Let us assume, x ∈ B So, x ∈ A ∪ B

x ∈ A ∪ C

Hence, x ∈ A or x ∈ C

when x ∈ A, then x ∈ B

∴ x ∈ A ∩ B

As, A ∩ B = A ∩ C

So, x ∈ A ∩ C

∴ x ∈ A or x ∈ C

x ∈ C

∴ B ⊂ C

similarly, it can be shown that C ⊂ B

Hence, B = C

Q12.Show that for any sets A and B

A = (A∩B)∪(A-B)

Ans.We have to prove

A = (A∩B)∪(A-B)

Taking RHS and solving it

(A∩B)∪(A-B)

Using the property

A -B = A -(A∩B)

A-B = A∩B’

= (A∩B) ∪ (A∩B’)

Applying distributive property

A∩(B∪C) = (A∩B) ∪(A∩C)

Replacing C = B’ in LHS

A-B = A∩(B∪B’)

= A∩ (U) [since B∪B’ = U]

= A [since A∩ U = A]

= RHS, Hence proved

Q13. Write the following sets in the roster form:

(i) A = {x : x ∈ R, 2x + 15 = 15}

(ii) B = {x : x² = x, x ∈ R}

Ans(i) It is given to us that set

A = {x : x ∈ R, 2x + 11 = 15}

2x + 11 = 15

2x = 15 – 11

2x = 4

x = 2

Therefore in roster form it is written as A = {2}

(ii) It is given to us that

B = {x : x² =x, x ∈ R}

x² = x

x² – x = 0

x(x – 1) = 0

x = 0, x = 1

Therefore in roster form it is written as

B = {0, 1}

Q14. If A and B are subsets of the universal set U, then show that

(i) A ⊂ A ∪ B

Ans. Let’s prove that

A ⊂ A ∪ B

Let x ∈ A or x ∈ B

If x ∈ A then x ∈ A ∪ B

Hence A ⊂ A ∪ B

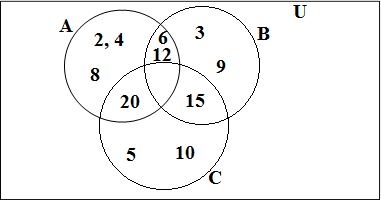
Q15. A,B and C are subsets of universal set if A = {2,4,6,8,12,20}, B ={3,6.9.12.15},C ={5,10,15,20} and U is the set of all whole numbers,draw a venn diagram showing the relation of U,A,B and C.

Ans.

Q16.If A and B are two sets such that A ⊂B then find:

(i) A ∩ B (ii) A ∪ B

Ans.(i) A ∩ B implies all the elements which are available in A and B

Let A = {1,2,3}, B = {1,2,3,4,5}⇒ A ⊂B

A ∩ B = {1,2.3} = A

∴A ∩ B = A

A ⊂B implies that all the elements of A are in B

(ii) A ∪ B implies all the elements which are available in A or B

Let A = {1,2,3}, B = {1,2,3,4,5}⇒ A ⊂B

A ∪ B = {1,2,3,4,5} = B

∴ A ∪ B = B

Q17.Let A ={{2,3,4},{5,6},{6,7,8}}.Determine which of the following is true or false.

(i) 4 ∈ A (ii) {2,3,4} ⊂ A (iii) {6,7,8}∈ A (iv) {5,6} ∈ A (v) Φ∈ A (vi) Φ ⊂ A

Ans. (i) False, since 4 is not an element of the set A, it is the part of the element {2,3,4}

(ii) False, {2,3,4} is an element of A,therefore it is written as {2,3,4}∈ A

(iii) True, since {6,7,8} is an element of A

(iv) True, since {5,6} is an element of A

(v) False,Φ is not an element of any set,it is a subset of every set

(vi) True, since Φ is a subset of every set

Class 11 Maths solutions of important questions of chapter 1-Sets

For complete questions download the following PDF

Download pdf of most important questions of 11 th class maths chapter 1-Sets with solutions

Class 11 Maths solutions of important questions of chapter 1-Sets pdf

You can compensate us

Paytm number 9891436286

The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.

Miscellaneous Exercise Chapter 1-Sets

NCERT solutins class 11 maths -Conic Section

NCERT Solutions Class 10 Science from chapter 1 to 16

What is differentiation?

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals