Class 11Physics Chapter 4 Circular Motion in a Plane

Examples of circular motion are the rotation of the earth around its own axis and the motion of the moon around the earth. there are two types of displacement in a circular motion, one is linear displacement and angular displacement .linear displacement is the length of the arc covered by an object is s and the radius of the circle is r then angular displacement is s/r radian, linear displacement divided by time results linear velocity and angular displacement divided by time results angular velocity.

 

Class 11Physics Chapter 4 Circular Motion in a Plane

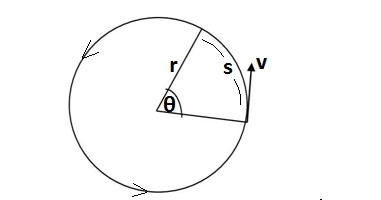
Let the angular displacement of a rotating object is θ and linear displacement is s

Angular displacement = Arc/Radius

θ = s/r

s =rθ, is the relationship between linear and angular displacement

Linear velocity =Linear displacement/Time

Let there is Δs change in linear displacement, change in angular displacement is Δθ in time Δt, then average velocity and average angular velocity are given by

Average linear velocity =Change in linear displacement/Change in time and Average angular displacement =Change in angular displacement/Change in time

v_av = Δs/Δt and w_av = Δθ/Δt

If Δt is infinitesimally small then corresponding linear displacement and angular displacement are ds and dθ then instantaneous linear velocity and instantaneous angular velocity is evaluated as following

v_ins = ds/dt and w_ins = dθ/dt

Angular velocity is an axial vector, so the direction of angular velocity is in outward of the plane. If the object is moving clockwise then the direction of angular velocity is otward of the plane and if the object is moving anticlockwise then the direction of angular velocity is inward of the plane.

The relationship between angular velocity and linear velocity:

The equations are known to us

v = Δs/Δt …..(i) w = Δθ/Δt…….(ii)

Dividing equation (i) by equation (ii)

v/w = Δs/ Δθ

Putting the value of

s =rθ

v/ω= Δ(rθ)/ Δθ

v/ω = r(Δθ)/ Δθ[ r is constant)

v = rω

Angular velocity of an object which is moving in a straight line:

Let there is a point B wherefrom we are going to observe the angular velocity of an object at A which is moving at the velocity of v in a straight line.

ω = v/r,here v and r should be perpendicular to each other

Now, let us consider the angular velocity at C, at point C the linear velocity remains the same as it is supposed that the object is moving with a uniform velocity v but its angular velocity changes with the change in the value of θ(i.e angular displacement)

For evaluating the value of angular velocity we have to consider the component of the velocity which is directed perpendicular to its distance from B(i.e r’) which is vcosθ

Therefore in this case the angular velocity will be

ω = vcosθ/r

Angular velocity of a moving object in a straight line with respect to another moving object:

Let the velocity of an object at A is v_A

and the velocity of another object which is at a distance of AB and moving with a velocity of  v_B by an angle θ with the distance AB

Angular velocity of the object B with respect to A = ω_BA

First of all let’s calculate the component of the linear velocity v_B which is perpendicular to the distance AB

The vertical component of v_B is =v_B sinθ

The relative velocity of the object B with respect to A = v_BA = v_B -v_A 

Forces and Newton’s First Laws of motion:Class 11 Physics Chapter 5 CBSE

Addition of Vectors: CBSE Class 11 Physics Chapter 4 -Motion in a Plane

Don’t forget to write a comment, subscribe us for the posts related to your study

Electronic Configuration of s,p and d orbitals

Atomic Radius Class 11 Chemistry Chapter 3 Periodicity in Properties

Why does a Rainbow look like a Bow?

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT Solutions for Class 11 Physics

Chapter 1- Physical World

chapter 3-Motion in a Straight Line

NCERT Solutions for Class 11 Chemistry

Chapter 1-Some basic concepts of chemistry

Chapter 2- Structure of Atom

NCERT Solutions for Class 11 Biology

Chapter 1 -Living World

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution