Projectile Motion Class 11 CBSE Physics Chapter 4 Motion in a Plane

Projectile motion is one of type of motion in a two-dimensional plane under an impact of gravitational force, it is the path of motion traversed by a thrown object towards the sky by an angle θ from the horizon. The path of the object is maintained by two components of the velocity, a vertical component towards the direction of the y-axis and a horizontal component towards the x-axis, both of these components are responsible to form a curved path of the object, such a motion is known as projectile motion.

Projectile Motion Class 11 CBSE Physics Chapter 4 Motion in a Plane

The path of the trajectory of the projectile is given as follows

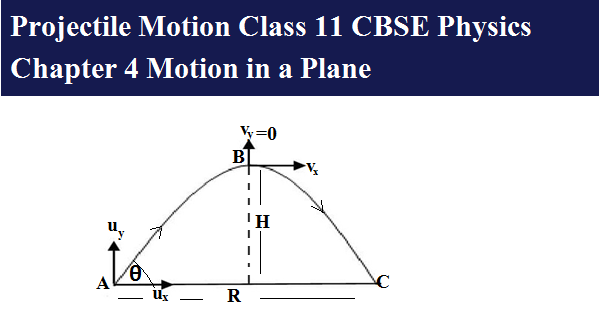
Let the angle of projection is θ, and the object is thrown with the u velocity, since the motion is in two-dimensional plane Y and X axis, therefore considering the two component of velocity one is towards the y-axis and another towards the x-axis.

Let the components of motion towards the y-axis is u_y and towards the x-axis is u_x

u_y = usinθ (vertical component of velocity)and u_x = ucosθ(horizontal component of velocity)

In this motion, acceleration is due to the gravity is along the y-axis,in x -direction its value is 0,a_x=0

Since there is no acceleration in the x direction, therefore the velocity u_x = ucosθ will remain constant and in the direction of y(i.e for the vertical component) the acceleration is always -g,a_y = -g

The initial velocity of the obect in y direction is usinθ and when it obtained maximum height H(i.e point B),the vertical component of velocity,v_y becomes 0,v_y = 0

From A to B the velocity of the object decreases and from B to C ,the velocity of the object decreases

Note: The parameters are considered in this motion supposing air resistance is zero

Let the time taken by the flight of the object is =T

Maximum height (the distance of point B from the ground)=H

The range of the object(horizontal distance from A to C)=R

Let’s consider the motion from A to B.

The maximum height of the object is gained due to the y component of the velocity

The initial y component of the velocity is u_y = usinθ and the final velocity (i.e at B) =V_y =0

Applying the first equation of the motion

v = u +at

0 = usinθ -gt

gt = usinθ

t = usinθ/g

The time taken from A to B and B to C will be the same due to the conservational law of energy

∴T = 2usinθ/g

Now applying third equation of the motion for determining maximum height of the projectile

v² = u² +2as

The initial y component of the velocity is u_y = usinθ and the final velocity (i.e at B) =V_y =0

0= (usinθ)² +2(-g)H

2gH = u²sin²θ

H = u²sin²θ/2g

Since the range, AC is in the horizontal direction, therefore, considering the horizontal component of the velocity

Initial velocity in the x-direction,u_x = ucosθ and final velocity(i.e at C) = v_x =0 ,acceleration along x axis is 0

Applying second equation of the motion

s = ut + (1/2) at²

R = ucosθ.T + (1/2) ×0×T²

Substituting the value of T

R = ucosθ.2usinθ/g

R = u²2cosθsinθ/g

R = u²sin 2θ/g

Circular Motion: Angular velocity and angular displacement

Addition of Vectors: CBSE Class 11 Physics Chapter 4 -Motion in a Plane

Don’t forget to write a comment, subscribe us for the posts related to your study

Electronic Configuration of s,p and d orbitals

Atomic Radius Class 11 Chemistry Chapter 3 Periodicity in Properties

Why does a Rainbow look like a Bow?

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution

Projectile Motion Class 11 CBSE Physics Chapter 4 Motion in a Plane

Projectile Motion Class 11 CBSE Physics Chapter 4 Motion in a Plane