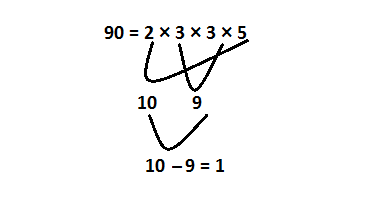The three ways of solving the quadratic equation
The Quadratic equations are very helpful in calculating the unknown variable. If we know tendency of a variable how does it vary, we can form a quadratic equation and solve it to get the unknown value. Quadratic equations are very useful in science, maths, economics, business, and accounts. Here three ways of solutions of a quadratic equation are beautifully explained by an expert of maths by step by step method so every student can understand it easily.
Future study point is doing his best in targetting the students who afraid of maths and are looking for the best maths tutor who could understand their problem, if you want to join science or commerce stream after 10 th pass then study with us we will make you fit for the subject, we are always in search of new ways of learning maths and science.
Studying our posts regularly will make you a hundred percent confident, enthusiastic, and conquerer. In this post, Future Study Point has brought the three ways of solving the quadratic equation. The solutions of questions are explained by three methods by the expert in such a way that even junior class students could understand it easily, though you are fully authorized to communicate with us by writing your comments in this blog, through e-mail, Facebook and WhatsApp if you face any problem.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Before we go through the post, first of all, understand what is the quadratic equation. the algebraic expression in the form of ax² + ax + c is known as a quadratic expression or any algebraic expression in which highest power of the variable is 2 then such an expression is known as quadratic expression as an example 3x², 9x² +2, the equation involving quadratic expression is known as the quadratic equation,as an example ax² + ax + c =0
Most popular mobile phones in Amazon: click here
The solution of this equation is determined by the factorizing quadratic expression thereby writing each factor equivalent to zero and then evaluating the value of the variable in the equation. The quadratic equation can be solved by factorization with the split-up method, By the complete square method and by using the quadratic formula See the example.
NCERT Solutions Class 10 Science from chapter 1 to 16
You can also study
Class 10 Biology Viva Voce Questions and Answers for CBSE Board 2020-21
Class 10 Physics Viva Voce Questions for CBSE Board 2020-21
Class 10 chemistry Viva Voce Questions and Answers for CBSE Board 2020-21
Class 10 Chemistry Practical Based Questions for CBSE 2020-21 Board Exam
Type of Chemical Reactions with Complete detail
Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry
Class 10 Maths NCERT solutions of Chapter 6- Triangles
Ozone Layer and How it is Getting depleted.
Solutions of Class 10 maths question paper Set-3 CBSE Board 2019
CBSE Class 10 science question paper 2020 SET -3 solutions
Science and Maths NCERT solutions for Class 9 ,10 and 11 classes
Example- Solve the quadratic equation 15x² + x – 6 = 0 .
Ans. 15x² + x – 6 = 0
We can solve this equation by factorizing the expression 15x² + x – 6
We can solve it by choosing one of the ways of factorization.
1 . SPLIT UP METHOD-
Determine two factors of the product 15 × 6 = 90 such that the product of factor is 90 and their addition or difference is 1.
15x² + x – 6 = 0
15x² + (10 – 9)x – 6 = 0
15x² + 10 x– 9x – 6 = 0
5x(3x + 2) – 3(3x + 2)= 0
(3x + 2)(5x – 3) = 0
3x + 2 = 0
3x = – 2
5x – 3 = 0
5x = 3
Therefore the solutions of the given equation are 3/5 and –2/3
2. Factorising by complete square-
The given expression can be transformed into the complete square as follows
15x² + x – 6 = 0
Complete square mean writing the given expression, 15x² + x – 6 into the form of (a + b)²
Step1- Make the square term 15x² a complete square by multiplying 15 to the whole of the equation
we get , 225x² +15 x – 90 =0
Step2-Rewrite the equation as follows
(15x)² + 15x – 90 = 0
Step3- Comparing it to complete square (a² +2ab + b²)
If 15x→a, ⇒ 2ab = 15x ⇒ b = 15x/2a = 15x/30x =1/2
Step3-Rewrite the equation as follows by adding and subtracting (1/2)²
(15x)² + 15x + (1/2)² – (1/2)²– 90 = 0
(15x + 1/2)² – 1/4 – 90 = 0
(15x + 1/2)² – 361/4 = 0
(15x + 1/2)² –(19/2)² = 0
(15x + 1/2 + 19/2)(15x + 1/2 – 19/2) = 0
(15x + 10)(15x – 9) = 0
(15x + 10) = 0 ⇒ x = –2/3 and (15x – 9)=0⇒ x = 3/5
Therefore the solutions of the given equation are –2/3 and 3/5.
3. Solution by the quadratic formula-
The solution of the equation of the form ax² + bx + c , can be completed by the following formula.
We have the following equation
15x² + x – 6 = 0, where a = 15, b = 1 and c = –6
Placing values a,b and c in the above formula
Therefore the solutions of the given equations are –2/3 and 3/5.
Friends tell us how did you like this post please don’t forget to write a comment
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT Solutions for Class 11 Physics
chapter 3-Motion in a Straight Line
NCERT Solutions for Class 11 Chemistry
Chapter 1-Some basic concepts of chemistry
NCERT Solutions for Class 11 Biology
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution